VnDoc.com

Tổng hợp công thức Dao động điều hòa đầy đủ và dễ nhớ

Công thức Vật lý 11

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Vật Lý

Dạng tài liệu: Chuyên đề

Mức độ: Trung bình

Loại File: PDF

Phân loại: Tài liệu Tính phí

Công thức Vật lý 11 Dao động điều hòa

Bạn đang tìm kiếm tài liệu tổng hợp công thức dao động điều hòa đầy đủ và dễ nhớ để phục vụ cho việc học tập hoặc ôn thi Vật Lý 11? Trong bài viết này, chúng tôi sẽ giúp bạn hệ thống lại toàn bộ các công thức quan trọng trong chuyên đề dao động điều hòa, được trình bày rõ ràng, dễ hiểu và dễ ghi nhớ. Tài liệu phù hợp với học sinh THPT, đặc biệt là các bạn đang chuẩn bị cho kỳ thi THPT Quốc Gia. Đừng bỏ lỡ bảng tóm tắt đầy đủ ở cuối bài nhé!

I. Dao động cơ

1. Thế nào là dao động cơ

Chuyển động qua lại quanh một vị trí đặc biệt, gọi là vị trí cân bằng.

2. Dao động tuần hoàn

Sau những khoảng thời gian bằng nhau gọi là chu kỳ, vật trở lại vị trí cũ theo hướng cũ.

II. Phương trình của dao động điều hòa

1. Định nghĩa: Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian

2. Phương trình dao động điều hòa

x = Acos( ωt + ϕ)

+ A là biên độ dao động ( A>0), A phụ thuộc năng lượng cung cấp cho hệ ban dầu, cách kích thích

+ ( ωt + ϕ ) là pha của dao động tại thời điểm t

+ ϕ là pha ban đầu, phụ tuộc cách chọn gốc thời gian,gốc tọa độ, chiều dương

III. Chu kỳ, tần số và tần số góc của dao động điều hòa

1. Chu kỳ, tần số

Chu kỳ T: Khoảng thời gian để vật thực hiện một dao động toàn phần – đơn vị giây (s)

Tần số f: Số dao động toàn phần thực hiện được trong một giây – đơn vị Héc (Hz)

2. Tần số góc

$\omega = \frac{2\pi}{T} = 2\pi f$ $\omega = \frac{2\pi}{T} = 2\pi f$; $f = \frac{1}{T}$ $f = \frac{1}{T}$ (ω, T, f chỉ phụ tuộc đặc tính của hệ)

VI. Vận tốc và gia tốc của vật dao động điều hòa

1. Công thức vận tốc dao động điều hòa

v = x’ = -ωAsin(ωt + ϕ ) = ω.Acos(ω.t + ϕ + π/2)

Ở vị trí biên: x = ± A ⇒ v = 0
Ở vị trí cân bằng: x = 0 ⇒ v_max = Aω
Liên hệ v và x: $x^{2} + \frac{v^{2}}{\omega^{2}} = A^{2}$ $x^{2} + \frac{v^{2}}{\omega^{2}} = A^{2}$
Liên hệ v và a : $\frac{a^{2}}{\omega^{4}} + \frac{v^{2}}{\omega^{2}} = A^{2}$ $\frac{a^{2}}{\omega^{4}} + \frac{v^{2}}{\omega^{2}} = A^{2}$

2. Công thức gia tốc dao động điều hòa

a = v’ = x”= -ω²Acos(ωt + ϕ ) = $\omega^{2}Acos(\omega t + \varphi + \pi)$ $\omega^{2}Acos(\omega t + \varphi + \pi)$

Ở vị trí biên: $|a|_{\max} = \omega^{2}A$ $|a|_{\max} = \omega^{2}A$
Ở vị trí cân bằng a = 0
Liên hệ a và x: a = - ω²x

3. Đồ thị của dao động điều hòa

Đồ thị biểu diễn sự phụ thuộc của x vào t là một đường hình sin.

4. Liên hệ giữa dao động điều hòa và chuyển động tròn đều

Một điểm dao động điều hòa trên một đoạn thẳng có thể coi là hình chiếu của một điểm tương ứng chuyển động tròn đều lên đường kính là đoạn thẳng đó.

5. Độ lệch pha của x, v, a

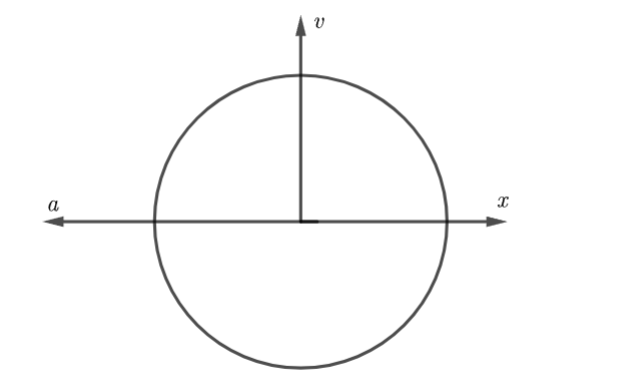
Lưu ý:

Khi 1 đại lượng biến thiên theo thời gian ở thời điểm t₀ tăng thì đạo hàm bậc nhất của nó theo t sẽ dương và ngược lại. (hoặc dùng vòng tròn lượng giác biết ngay là tại thời điểm t đại lượng nào đó đang tăng hoặc giảm.
Góc ϕ > 0 ứng với nửa đường tròn phía trên, đại lượng đó đang giảm và ngược lại)

V. Các dạng bài tập dao động điều hòa

1. Dao động có phương trình đặc biệt:

x = a ± Acos(ωt + ϕ) với a = const

Biên độ là A, tần số góc là ω, pha ban đầu ϕ; x là toạ độ, x₀ = Acos(ωt + ϕ) là li độ.

Toạ độ vị trí cân bằng x = a, toạ độ vị trí biên x = a ± A
Vận tốc v = x’ = x₀’, gia tốc a = v’ = x” = x₀”
Hệ thức độc lập: a = -ω²x₀
$A^{2} = x_{0}^{2} + (\frac{v}{\omega})^{2}$ $A^{2} = x_{0}^{2} + (\frac{v}{\omega})^{2}$

x = a ± Acos²(ωt + ϕ) (ta hạ bậc). Biên độ A/2; tần số góc 2ω, pha ban đầu 2ϕ.

2. Chiều dài quỹ đạo: 2A

3. Quãng đường đi trong 1 chu kỳ luôn là 4A; trong 1/2 chu kỳ luôn là 2A

Quãng đường đi trong l/4 chu kỳ là A khi vật đi từ VTCB đến vị trí biên hoặc ngược lại

Thời gian vật đi được những quãng đường đặc biệt:

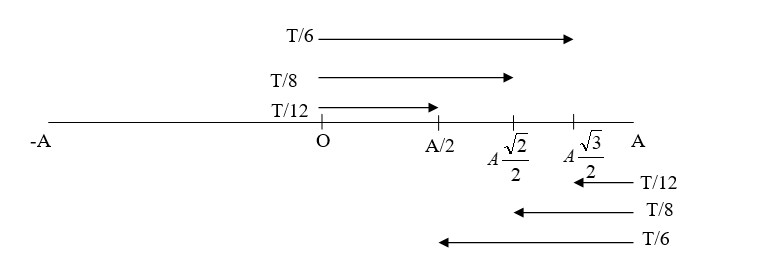
4. Các bước lập phương trình dao động dao động điều hoà

* Tính ω

* Tính A

* Tính ϕ dựa vào điều kiện đầu: lúc t = t₀ (thường t₀ = 0)

$\left\{ \begin{matrix} x = Acos(\omega t_{0} + \varphi) \\ v = - \omega Asin(\omega t_{0} + \varphi) \\ \end{matrix} \right.\ \Rightarrow \varphi$ $\left\{ \begin{matrix} x = Acos(\omega t_{0} + \varphi) \\ v = - \omega Asin(\omega t_{0} + \varphi) \\ \end{matrix} \right.\ \Rightarrow \varphi$

Lưu ý:

+ Vật chuyển động theo chiều dương thì v > 0 (ϕ < 0), ngược lại v < 0 (ϕ > 0)

+ Trước khi tính ϕ cần xác định rõ ϕ thuộc góc phần tư thứ mấy của đường tròn lượng giác (thường lấy -π < ϕ ≤ π).

5. Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ x₁ đến x₂: viết phương trình chuyển động chọn gốc thời gian lúc

x= x₁, v > 0, thay x= x₂, v > 0 tìm t

6. Quãng đường vật đi được từ thời điểm t₁ đến t₂.

Phân tích: t₂ – t₁ = nT + ∆t (n ∈N; 0 ≤ ∆t < T)

Quãng đường đi được trong thời gian nT là S₁ = 4nA, trong thời gian ∆t là S₂.

Quãng đường tổng cộng là S = S₁ + S₂

+ Tính S₂ bằng cách định vị trí x₁, x₂ và chiều chuyển động của vật trên trục Ox

Xác định: $\left\{ \begin{matrix} x_{1} = Acos(\omega t_{1} + \varphi) \\ v_{1} = - \omega Asin(\omega t_{1} + \varphi) \end{matrix} \right.$ $\left\{ \begin{matrix} x_{1} = Acos(\omega t_{1} + \varphi) \\ v_{1} = - \omega Asin(\omega t_{1} + \varphi) \end{matrix} \right.$ và $\left\{ \begin{matrix} x_{2} = Acos(\omega t_{2} + \varphi) \\ v_{2} = - \omega Asin(\omega t_{2} + \varphi) \end{matrix} \right.$ $\left\{ \begin{matrix} x_{2} = Acos(\omega t_{2} + \varphi) \\ v_{2} = - \omega Asin(\omega t_{2} + \varphi) \end{matrix} \right.$ (v₁ và v₂ chỉ cần xác định dấu)

Lưu ý: + Nếu ∆t = T/2 thì S₂ = 2A

+ Tốc độ trung bình của vật đi từ thời điểm t₁ đến t₂: $v_{tb} = \frac{S}{t_{2} - t_{1}}$ $v_{tb} = \frac{S}{t_{2} - t_{1}}$ với S là quãng đường tính như trên.

7. Tính thời gian đi được quãng đường S và thời gian vật đi từ li độ x₁ đến x₂ cũng tương tự:

Phân tích :S = n4A + ∆S

- Thời gian đi được quãng đường n.4A là t = n.T

- Nếu ∆S= 2A thì t’=T/2

- Nếu ∆S lẻ thì tìm thời gian vật đi từ li độ x₁ đến x_{2 là} t’

* Toàn bộ thời gian là: t+t’

8. Các bước giải bài toán tính thời điểm vật đi qua vị trí đã biết x (hoặc v, a, W_t, W_đ, F) lần thứ n

* Giải phương trình lượng giác lấy các nghiệm của t (Với t > 0 ⇒ phạm vi giá trị của k)

* Liệt kê n nghiệm đầu tiên (thường n nhỏ)

* Thời điểm thứ n chính là giá trị lớn thứ n

9. Các bước giải bài toán tìm số lần vật đi qua vị trí đã biết x (hoặc v, a, W_t, W_đ, F) từ thời điểm t₁ đến t₂.

* Giải phương trình lượng giác được các nghiệm

* Từ t₁ < t ≤ t₂ ⇒ Phạm vi giá trị của (Với k ∈ Z)

* Tổng số giá trị của k chính là số lần vật đi qua vị trí đó.

Lưu ý:

+ Có thể giải bài toán bằng cách sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều.

+ Trong mỗi chu kỳ (mỗi dao động) vật qua mỗi vị trí biên 1 lần còn các vị trí khác 2 lần.

10. Các bước giải bài toán tìm li độ, vận tốc dao động sau (trước) thời điểm t một khoảng thời gian ∆t.

Biết tại thời điểm t vật có li độ x = x₀.

+Viết lại phương trình chuyển động, chọn gốc thời gian là x = x₀. v>o (hoặc v<0 tùy theo đề)

Thế t = ∆t tìm được đại lượng cần

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

-------------------------------

Trên đây là toàn bộ công thức dao động điều hòa cần nhớ trong chương trình Vật Lý 11. Hy vọng tài liệu này sẽ giúp bạn hệ thống kiến thức hiệu quả, tự tin hơn khi giải các dạng bài tập và đạt điểm cao trong các kỳ thi. Đừng quên lưu lại bài viết hoặc tải file PDF tổng hợp để tiện ôn tập bất cứ lúc nào. Nếu bạn thấy bài viết hữu ích, hãy chia sẻ cho bạn bè cùng học nhé!

Tải về

Chọn file muốn tải về: