VnDoc.com

Tại 2 điểm A và B cách nhau 10cm trong không khí

Bài tập điện trường Vật lý 11 có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Vật Lý

Dạng tài liệu: Chuyên đề

Mức độ: Trung bình

Loại File: Word

Phân loại: Tài liệu Tính phí

Cách tính cường độ điện trường tại 2 điểm A và B

Trong chương Điện trường – Vật lý 11, dạng toán về các điểm A, B trong không khí là dạng bài cơ bản nhưng quan trọng, thường xuất hiện trong đề kiểm tra và đề thi THPT Quốc gia. Đặc biệt, bài tập Tại 2 điểm A và B cách nhau 10cm trong không khí giúp học sinh rèn luyện kỹ năng vận dụng công thức cường độ điện trường, lực tương tác giữa các điện tích để giải quyết tình huống thực tế. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu kèm theo công thức cần nhớ, hỗ trợ học sinh ôn tập hiệu quả.

A. Phương pháp chung

Gọi $\overrightarrow{E_{1}},\overrightarrow{E_{2}},\overrightarrow{E_{3}},...$ $\overrightarrow{E_{1}},\overrightarrow{E_{2}},\overrightarrow{E_{3}},...$ là điện trường do điện tích $q_{1},q_{2},q_{3},...$ $q_{1},q_{2},q_{3},...$ gây ra tại điểm M.

Cường độ điện trường tổng hợp tại M do $q_{1},q_{2},q_{3},...$ $q_{1},q_{2},q_{3},...$ gây ra là:

$\boxed{\overrightarrow{E} = \overrightarrow{E_{1}} + \overrightarrow{E_{2}} + \overrightarrow{E_{3}} + ...}$ $\boxed{\overrightarrow{E} = \overrightarrow{E_{1}} + \overrightarrow{E_{2}} + \overrightarrow{E_{3}} + ...}$

Thông thường ta sẽ gặp hai hoặc ba điện tích gây ra điện trường tại điểm M.

Công thức cường độ điện trường

Độ lớn: $\boxed{E = k\frac{|q|}{\varepsilon r^{2}}}$ $\boxed{E = k\frac{|q|}{\varepsilon r^{2}}}$

Trong đó $k = 9.10^{9}\left( Nm^{2}/C^{2} \right)$ $k = 9.10^{9}\left( Nm^{2}/C^{2} \right)$

$|q|$ là độ lớn của điện tích điểm (C).

$\varepsilon$ $\varepsilon$ là hằng số điện môi của môi trường.

r là khoảng cách từ điện tích điểm đến điểm ta xét (m).

- Có hai điện tích cùng dấu, muốn điện tích thứ ba có cường độ điện trường tổng hợp bằng 0 thì điện tích đó phải đặt ở vị trí thuộc đoạn thẳng nối hai điện tích.

- Có hai điện tích trái dấu, muốn điện tích thứ ba có cường độ điện trường tổng hợp bằng 0 thì điện tích đó phải đặt ở vị trí nằm trên đường thẳng đi qua hai điện tích và ngoài đoạn thẳng nối hai điện tích.

B. Bài tập ví dụ minh họa tính Lực điện trường tác dụng lên điện tích

Ví dụ 1: Tại 2 điểm A và B cách nhau 10 cm trong không khí có đặt 2 điện tích $q_{1} = q_{2} = 16.10^{- 8}\ C$ $q_{1} = q_{2} = 16.10^{- 8}\ C$. Xác định cường độ điện trường do hai điện tích này gây ra tại điểm C biết $AC = BC = 8\ cm$ $AC = BC = 8\ cm$. Xác định lực điện trường tác dụng lên điện tích $q_{3} = 2.10^{- 6}\ C$ $q_{3} = 2.10^{- 6}\ C$ đặt tại C.

A. 0,6 N. B. 0,5 N. C. 0,35 N. D. 0,7 N.

Hướng dẫn giải

Cách 1: Làm theo phương pháp sử dụng tổng hợp các lực tĩnh điện do các điện tích tác dụng lên điện tích $q_{3}$ $q_{3}$.

Cách 2: Tính cường độ điện trường tổng hợp gây ra tại điểm C và sử dụng biểu thức $F = |q|E$.

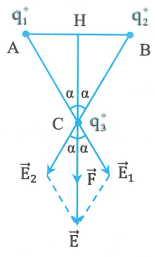
Các điện tích $q_{1}$ $q_{1}$ và $q_{2}$ $q_{2}$ gây ra tại c các véc tơ cường độ điện trường $\overrightarrow{E_{1}}$ $\overrightarrow{E_{1}}$ và $\overrightarrow{E_{2}}$ $\overrightarrow{E_{2}}$ có phương chiều như hình vẽ, có độ lớn:

$E_{1} = E_{2} = k\frac{\left| q_{1} \right|}{AC^{2}} = 9.10^{9}\frac{\left| q_{1} \right|}{AC^{2}} = 225.10^{3}q_{1}(V/m)$ $E_{1} = E_{2} = k\frac{\left| q_{1} \right|}{AC^{2}} = 9.10^{9}\frac{\left| q_{1} \right|}{AC^{2}} = 225.10^{3}q_{1}(V/m)$

Cường độ điện trường tổng hợp tại C do các điện tích $q_{1}$ $q_{1}$ và $q_{2}$ $q_{2}$ gây ra là:

$\overrightarrow{E} = \overrightarrow{E_{1}} + \overrightarrow{E_{2}}$ $\overrightarrow{E} = \overrightarrow{E_{1}} + \overrightarrow{E_{2}}$ có phương chiều như hình vẽ và có độ lớn:

$E = E_{1}\cos\alpha + E_{2}\cos\alpha = 2E_{1}\cos\alpha = 2E_{1}\frac{\sqrt{AC^{2} - AH^{2}}}{AC} \approx 351.10^{3}(V/m)$ $E = E_{1}\cos\alpha + E_{2}\cos\alpha = 2E_{1}\cos\alpha = 2E_{1}\frac{\sqrt{AC^{2} - AH^{2}}}{AC} \approx 351.10^{3}(V/m)$

Lực điện trường tổng hợp do $q_{1}$ $q_{1}$ và $q_{2}$ $q_{2}$ tác dụng lên $q_{3}$ $q_{3}$ có độ lớn

$F = \left| q_{3} \right|E = 0,7N$ $F = \left| q_{3} \right|E = 0,7N$.

Đáp án D.

Ví dụ 2: Tại hai điểm A và B cách nhau 10 cm trong không khí có đặt hai điện tích $q_{1} = - q_{2} = 6.10^{- 6}\ C$ $q_{1} = - q_{2} = 6.10^{- 6}\ C$. Xác định cường độ điện trường do hai điện tích này gây ra tại điểm C biết $AC = BC = 12\ cm$ $AC = BC = 12\ cm$. Tính lực điện trường tác dụng lên điện tích $q_{3} = - 3.10^{- 8}\ C$ $q_{3} = - 3.10^{- 8}\ C$ đặt tại C.

A. 0,094 N. B. 0,025 N. C. 0,048 N. D. 0,7 N.

Hướng dẫn giải

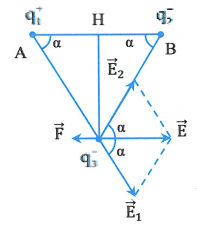
Các điện tích $q_{1}$ $q_{1}$ và $q_{2}$ $q_{2}$ gây ra tại c các vectơ cường độ điện trường $\overrightarrow{E_{1}}$ $\overrightarrow{E_{1}}$ và $\overrightarrow{E_{2}}$ $\overrightarrow{E_{2}}$ có phương chiều như hình vẽ, có độ lớn:

$E_{1} = E_{2} = k\frac{\left| q_{1} \right|}{AC^{2}} = 9.10^{9}\frac{\left| q_{1} \right|}{AC^{2}} = 375.10^{4}(V/m)$ $E_{1} = E_{2} = k\frac{\left| q_{1} \right|}{AC^{2}} = 9.10^{9}\frac{\left| q_{1} \right|}{AC^{2}} = 375.10^{4}(V/m)$

Cường độ điện trường tổng hợp tại C do các điện tích $q_{1}$ $q_{1}$ và $q_{2}$ $q_{2}$ gây ra là: $\overrightarrow{E} = \overrightarrow{E_{1}} + \overrightarrow{E_{2}}$ $\overrightarrow{E} = \overrightarrow{E_{1}} + \overrightarrow{E_{2}}$ có phương chiều như hình vẽ và có độ lớn:

$E = E_{1}\cos\alpha + E_{2}\cos\alpha = 2E_{1}\cos\alpha = 2E_{1}\frac{AH}{AC} = 312,5.10^{4}(V/m)$ $E = E_{1}\cos\alpha + E_{2}\cos\alpha = 2E_{1}\cos\alpha = 2E_{1}\frac{AH}{AC} = 312,5.10^{4}(V/m)$

Lực điện trường tổng hợp do $q_{1}$ $q_{1}$ và $q_{3}$ $q_{3}$ tác dụng lên $q_{3}$ $q_{3}$ là: $\overrightarrow{F} = q_{3}\overrightarrow{E}$ $\overrightarrow{F} = q_{3}\overrightarrow{E}$.

Vì $q_{3} < 0$ $q_{3} < 0$, nên $\overrightarrow{F}$ $\overrightarrow{F}$ cùng phương ngược chiều với $\overrightarrow{E}$ $\overrightarrow{E}$ và có độ lớn:

$F = \left| q_{3} \right|E = 0,094\ \ (N)$ $F = \left| q_{3} \right|E = 0,094\ \ (N)$.

Đáp án A.

Ví dụ 3: Tại 2 điểm A, B cách nhau 20 cm trong không khí có đặt 2 điện tích $q_{1} = 4.10^{- 6}C$ $q_{1} = 4.10^{- 6}C$, $q_{2} = - 6,4.10^{- 6}C$ $q_{2} = - 6,4.10^{- 6}C$. Xác định cường độ điện trường do hai điện tích này gây ra tại điểm C biết $AC = 12\ cm$ $AC = 12\ cm$; $BC = 16\ cm$ $BC = 16\ cm$. Xác định lực điện trường tác dụng lên $q_{3} = - 5.10^{- 8}\ C$ $q_{3} = - 5.10^{- 8}\ C$ đặt tại C.

A. 0,1 N. B. 0,25 N. C. 0,34N. D. 0,17N.

Hướng dẫn giải

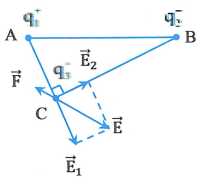
Tam giác ABC vuông tại C. Các điện tích $q_{1}$ $q_{1}$ và $q_{2}$ $q_{2}$ gây ra tại c các véc tơ cường độ điện trường $\overrightarrow{E_{1}}$ $\overrightarrow{E_{1}}$ và $\overrightarrow{E_{2}}$ $\overrightarrow{E_{2}}$ có phương chiều như hình vẽ, có độ lớn:

$E_{1} = k\frac{\left| q_{1} \right|}{AC^{2}} = 9.10^{9}\frac{\left| q_{1} \right|}{AC^{2}} = 25.10^{5}(V/m)$ $E_{1} = k\frac{\left| q_{1} \right|}{AC^{2}} = 9.10^{9}\frac{\left| q_{1} \right|}{AC^{2}} = 25.10^{5}(V/m)$.

$E_{2} = k\frac{\left| q_{2} \right|}{BC^{2}} = 9.10^{9}\frac{\left| q_{2} \right|}{BC^{2}} = 22,5.10^{5}(V/m)$ $E_{2} = k\frac{\left| q_{2} \right|}{BC^{2}} = 9.10^{9}\frac{\left| q_{2} \right|}{BC^{2}} = 22,5.10^{5}(V/m)$.

Cường độ điện trường tổng hợp tại c do các điện tích $q_{1}$ $q_{1}$ và $q_{2}$ $q_{2}$ gây ra là: $\overrightarrow{E} = \overrightarrow{E_{1}} + \overrightarrow{E_{2}}$ $\overrightarrow{E} = \overrightarrow{E_{1}} + \overrightarrow{E_{2}}$ có phương chiều như hình vẽ và có độ lớn:

$E = \sqrt{E_{1}^{2} + E_{2}^{2}} \approx 33,6.10^{5}(V/m)$ $E = \sqrt{E_{1}^{2} + E_{2}^{2}} \approx 33,6.10^{5}(V/m)$.

Lực điện trường tổng hợp do $q_{1}$ $q_{1}$ và $q_{3}$ $q_{3}$ tác dụng lên $q_{3}$ $q_{3}$ là: $\overrightarrow{F} = q_{3}\overrightarrow{E}$ $\overrightarrow{F} = q_{3}\overrightarrow{E}$

Vì $q_{3} < 0$ $q_{3} < 0$, nên $\overrightarrow{F}$ $\overrightarrow{F}$ cùng phương ngược chiều với $\overrightarrow{E}$ $\overrightarrow{E}$ và có độ lớn:

$F = \left| q_{3} \right|E = 0,17\ \ (N)$ $F = \left| q_{3} \right|E = 0,17\ \ (N)$.

Đáp án D.

C. Bài tập tự rèn luyện có đáp án chi tiết

Bài 1: Tại hai điểm A và B cách nhau 10 cm trong không khí có đặt hai điện tích $q_{1} = - 1,6.10^{- 6}C$ $q_{1} = - 1,6.10^{- 6}C$ và $q_{2} = - 2,4.10^{- 6}C$ $q_{2} = - 2,4.10^{- 6}C$. Xác định cường độ điện trường do 2 điện tích này gây ra tại điểm C. Biết $AC = 8\ cm$ $AC = 8\ cm$; $BC = 6\ cm$ $BC = 6\ cm$.

A. $E = 64.10^{5}\ \ (V/m).$ $E = 64.10^{5}\ \ (V/m).$ B. $E = 32\sqrt{2}.10^{5}\ \ (V/m).$ $E = 32\sqrt{2}.10^{5}\ \ (V/m).$

C. $E = 32.10^{5}\ \ (V/m).$ $E = 32.10^{5}\ \ (V/m).$ D. $E = 32\sqrt{3}.10^{5}\ \ (V/m).$ $E = 32\sqrt{3}.10^{5}\ \ (V/m).$

Bài 2: Tại hai điểm A, B cách nhau 15 cm trong không khí có đặt hai điện tích $q_{1} = - 12.10^{- 6}C$ $q_{1} = - 12.10^{- 6}C$, $q_{2} = 2,5.10^{- 6}C$ $q_{2} = 2,5.10^{- 6}C$.

a) Xác định cường độ điện trường do hai điện tích này gây ra tại điểm C. Biết $AC = 20\ cm$ $AC = 20\ cm$; $BC = 5\ cm$ $BC = 5\ cm$.

A. $E = 81.10^{5}\ (V/m).$ $E = 81.10^{5}\ (V/m).$ B. $E = 63.10^{5}\ (V/m).$ $E = 63.10^{5}\ (V/m).$

C. $E = 94.10^{5}\ (V/m).$ $E = 94.10^{5}\ (V/m).$ D. $E = 86.10^{5}\ (V/m).$ $E = 86.10^{5}\ (V/m).$

b) Xác định vị trí điểm M mà tại đó cường độ điện trường tổng hợp do hai điện tích này gây ra bằng 0.

A. M là trung điểm của AB.

B. M thuộc đường thẳng AB, nằm cách A $6\sqrt{30}\ \ cm$ $6\sqrt{30}\ \ cm$ và cách B $6\sqrt{30} - 15\ \ cm$ $6\sqrt{30} - 15\ \ cm$.

C. M thuộc đường thẳng AB, nằm cách A 15 cm và cách B 30 cm.

D. M thuộc đường thẳng AB, nằm cách A 5 cm và cách B 10 cm.

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

-------------------------------------------------

Với bài toán “Tại 2 điểm A và B cách nhau 10cm trong không khí”, học sinh không chỉ củng cố kiến thức về cường độ điện trường và lực tương tác điện mà còn rèn luyện khả năng phân tích, suy luận logic để giải nhanh và chính xác. Đây là dạng bài tập điển hình trong phần Bài tập điện trường Vật lý 11 có đáp án, giúp bạn chuẩn bị vững vàng cho các bài kiểm tra, thi học kỳ và kỳ thi THPT Quốc gia.
👉 Hãy tiếp tục luyện tập với các dạng bài khác trong chuyên đề Điện trường Vật lý 11, kết hợp ghi nhớ công thức để đạt hiệu quả học tập cao nhất.

File word

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Ma Kết

1

15

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!