Đặt 4 điện tích có cùng độ lớn q tại 4 đỉnh của một hình vuông ABCD
Tính lực điện giữa các điện tích ở 4 đỉnh hình vuông
Trong chuyên đề Điện trường – Vật lý 11, bài toán “Đặt 4 điện tích có cùng độ lớn q tại 4 đỉnh của một hình vuông ABCD” là dạng nâng cao, giúp học sinh rèn luyện tư duy logic và khả năng vận dụng công thức tính lực điện, cường độ điện trường trong không gian. Đây là dạng toán thường gặp trong đề kiểm tra và đề thi THPT Quốc gia, đòi hỏi học sinh phải biết kết hợp kiến thức hình học với công thức vật lý để tìm ra lời giải nhanh và chính xác. Bài viết dưới đây sẽ cung cấp lời giải chi tiết kèm công thức để bạn ôn tập hiệu quả.
A. Bài tập minh họa có hướng dẫn
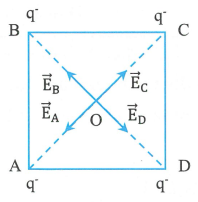
Bài tập 1: Đặt 4 điện tích có cùng độ lớn q tại 4 đỉnh của một hình vuông ABCD cạnh a với điện tích dương đặt tại A và C, điện tích âm đặt tại B và D. Xác định cường độ tổng hợp tại giao điểm hai đường chéo của hình vuông.
A. ![]() \(E = \frac{8kq}{\varepsilon
a^{2}}.\) B.
\(E = \frac{8kq}{\varepsilon
a^{2}}.\) B. ![]() \(E =
\frac{4\sqrt{3}kq}{\varepsilon a^{2}}.\) C.
\(E =
\frac{4\sqrt{3}kq}{\varepsilon a^{2}}.\) C. ![]() \(E = \frac{4\sqrt{2}kq}{\varepsilon
a^{2}}.\) D.
\(E = \frac{4\sqrt{2}kq}{\varepsilon
a^{2}}.\) D. ![]() \(E = 0.\)
\(E = 0.\)
Hướng dẫn giải
Các điện tích đặt tại các đỉnh của hình vuông gây ra tại giao điểm O của hai đường chéo hình vuông các véc tơ cường độ điện trường ![]() \(\overrightarrow{E_{A}};\ \
\overrightarrow{E_{B}};\ \ \overrightarrow{E_{C}};\ \
\overrightarrow{E_{D}}\) có phương chiều như hình vẽ, có độ lớn:
\(\overrightarrow{E_{A}};\ \
\overrightarrow{E_{B}};\ \ \overrightarrow{E_{C}};\ \
\overrightarrow{E_{D}}\) có phương chiều như hình vẽ, có độ lớn:
![]() \(E_{A} = E_{B} = E_{C} = E_{D} =
\frac{2kq}{\varepsilon a^{2}}.\)
\(E_{A} = E_{B} = E_{C} = E_{D} =
\frac{2kq}{\varepsilon a^{2}}.\)
Cường độ điện tường tổng hợp tại O là:
![]() \(\overrightarrow{E} =
\overrightarrow{E_{A}} + \overrightarrow{E_{B}} + \overrightarrow{E_{C}}
+ \overrightarrow{E_{D}} = \overrightarrow{0}\) (vì
\(\overrightarrow{E} =
\overrightarrow{E_{A}} + \overrightarrow{E_{B}} + \overrightarrow{E_{C}}
+ \overrightarrow{E_{D}} = \overrightarrow{0}\) (vì ![]() \(\overrightarrow{E_{A}} + \overrightarrow{E_{C}} =
\overrightarrow{0}\) và
\(\overrightarrow{E_{A}} + \overrightarrow{E_{C}} =
\overrightarrow{0}\) và ![]() \(\overrightarrow{E_{B}} + \overrightarrow{E_{D}} =
\overrightarrow{0}\)).
\(\overrightarrow{E_{B}} + \overrightarrow{E_{D}} =
\overrightarrow{0}\)).
Đáp án D.
Bài tập 2: Ba điện tích ![]() \(q_{1},q_{2},q_{3}\) đặt trong không khí lần lượt tại các đỉnh A, B, C của hình vuông ABCD. Biết véctơ cường độ điện trường tổng hợp tại D có giá là cạnh CD. Quan hệ giữa 3 điện tích trên là:
\(q_{1},q_{2},q_{3}\) đặt trong không khí lần lượt tại các đỉnh A, B, C của hình vuông ABCD. Biết véctơ cường độ điện trường tổng hợp tại D có giá là cạnh CD. Quan hệ giữa 3 điện tích trên là:
A. ![]() \(q_{1} = q_{2} = q_{3}\) B.
\(q_{1} = q_{2} = q_{3}\) B. ![]() \(q_{1} = - q_{2} = q_{3}\)
\(q_{1} = - q_{2} = q_{3}\)
C. ![]() \(q_{2} = - 2\sqrt{2}q_{1}\) D.
\(q_{2} = - 2\sqrt{2}q_{1}\) D. ![]() \(q_{3} = - 2\sqrt{2}q_{2}\)
\(q_{3} = - 2\sqrt{2}q_{2}\)
Hướng dẫn giải
+ Để vectơ cường độ điện trường tổng hợp tại D có giá là cạnh CD thì vectơ tổng hợp của ![]() \(\overrightarrow{E_{A}}\),
\(\overrightarrow{E_{A}}\), ![]() \(\overrightarrow{E_{B}}\) phải nằm trên CD tức là 2 điện tích
\(\overrightarrow{E_{B}}\) phải nằm trên CD tức là 2 điện tích ![]() \(q_{2}\),
\(q_{2}\), ![]() \(q_{1}\) phải trái dấu nhau.
\(q_{1}\) phải trái dấu nhau.
+ Mặt khác góc ![]() \(\widehat{BDC} =
45^{0}\) nên
\(\widehat{BDC} =
45^{0}\) nên ![]() \(E_{2} =
\sqrt{2}E_{1}\)
\(E_{2} =
\sqrt{2}E_{1}\)
![]() \(\Rightarrow \sqrt{2}\frac{k\left| q_{1}
\right|}{AD^{2}} = \frac{k\left| q_{2} \right|}{BD^{2}} \Rightarrow
\frac{\left| q_{2} \right|}{\left| q_{1} \right|} =
\sqrt{2}\frac{BD^{2}}{AD^{2}} = 2\sqrt{2}\)
\(\Rightarrow \sqrt{2}\frac{k\left| q_{1}
\right|}{AD^{2}} = \frac{k\left| q_{2} \right|}{BD^{2}} \Rightarrow
\frac{\left| q_{2} \right|}{\left| q_{1} \right|} =
\sqrt{2}\frac{BD^{2}}{AD^{2}} = 2\sqrt{2}\)
Mà 2 điện tích này trái dấu nhau ![]() \(\Rightarrow q_{2} = - 2\sqrt{2}q_{1}\)
\(\Rightarrow q_{2} = - 2\sqrt{2}q_{1}\)
Bài tập 3: Bốn điện tích điểm cùng độ lớn cùng dấu q đặt tại bốn đỉnh của hình vuông cạnh a. Xác định cường độ điện trường gây ra bởi bốn điện tích đó tại tâm của hình vuông:
A. ![]() \(E = 2k\frac{q}{a^{2}}\) B.
\(E = 2k\frac{q}{a^{2}}\) B. ![]() \(E = 4k\frac{q\sqrt{2}}{a^{2}}\) C. 0 D.
\(E = 4k\frac{q\sqrt{2}}{a^{2}}\) C. 0 D. ![]() \(E = k\frac{q\sqrt{3}}{a^{2}}\)
\(E = k\frac{q\sqrt{3}}{a^{2}}\)
Hướng dẫn giải
+ Vì bốn điện tích điểm cùng dấu cùng độ lớn nên tại tâm của hình vuông cường độ điện trường gây ra bởi bốn điện tích đó bằng 0
B. Bài tập vận dụng có đáp án
Bài tập 1: Bốn điện tích điểm cùng độ lớn q, hai điện tích dương và hai điện tích âm, đặt tại bốn đỉnh của hình vuông cạnh a, các điện tích cùng dấu kề nhau. Xác định cường độ điện trường gây ra bởi bốn điện tích đó tại tâm của hình vuông:
A. ![]() \(E = 2k\frac{q\sqrt{3}}{a^{2}}\) B.
\(E = 2k\frac{q\sqrt{3}}{a^{2}}\) B. ![]() \(E = k\frac{q\sqrt{3}}{a^{2}}\) C.
\(E = k\frac{q\sqrt{3}}{a^{2}}\) C. ![]() \(E = k\frac{q\sqrt{3}}{2a^{2}}\) D.
\(E = k\frac{q\sqrt{3}}{2a^{2}}\) D. ![]() \(E = 4k\frac{q\sqrt{2}}{a^{2}}\)
\(E = 4k\frac{q\sqrt{2}}{a^{2}}\)
Bài tập 2: Đặt 4 điện tích có cùng độ lớn q tại 4 đỉnh của một hình vuông ABCD cạnh a với điện tích dương đặt tại A và D, điện tích âm đặt tại B và C. Xác định cường độ điện trường tổng hợp tại giao điểm hai đường chéo của hình vuông.
A. ![]() \(E = \frac{8kq}{\varepsilon
a^{2}}.\) B.
\(E = \frac{8kq}{\varepsilon
a^{2}}.\) B. ![]() \(E =
\frac{4\sqrt{3}kq}{\varepsilon a^{2}}.\) C.
\(E =
\frac{4\sqrt{3}kq}{\varepsilon a^{2}}.\) C. ![]() \(E = \frac{4\sqrt{2}kq}{\varepsilon
a^{2}}.\) D.
\(E = \frac{4\sqrt{2}kq}{\varepsilon
a^{2}}.\) D. ![]() \(E = 0.\)
\(E = 0.\)
Không thể hiển thị hết nội dung tại đây — bấm Tải về để lấy toàn bộ tài liệu.
-----------------------------------------------------------
Qua bài toán “Đặt 4 điện tích có cùng độ lớn q tại 4 đỉnh của một hình vuông ABCD”, học sinh không chỉ củng cố kiến thức về nguyên lý chồng chất điện trường, lực tác dụng giữa các điện tích điểm mà còn nâng cao kỹ năng suy luận, trình bày lời giải khoa học. Đây là một trong những dạng toán trọng tâm của phần Bài tập điện trường Vật lý 11 có đáp án, hỗ trợ hiệu quả cho quá trình ôn tập thi học kỳ và ôn thi THPT Quốc gia.
👉 Hãy tiếp tục rèn luyện nhiều dạng toán khác về điện tích điểm, cường độ điện trường và lực điện để đạt kết quả học tập cao nhất.











