Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Cho hình thang ABCD vuông tại A và D

Các trường hợp đồng dạng của tam giác vuông

Tam giác đồng dạng lớp 8

A. Lí thuyết cần nhớ
B. Bài tập ví dụ minh họa
C. Bài tập tự rèn luyện

Các trường hợp đồng dạng của tam giác vuông là tài liệu ôn tập với các bài tập Toán lớp 8, giúp các bạn học sinh học tốt Toán 8 và luyện tập các dạng Toán lớp 8 đạt kết quả tốt nhất, góp phần củng cố thêm kiến thức của các bạn học sinh.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 8, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 8 sau: Nhóm Tài liệu học tập lớp 8. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Tam giác đồng dạng Toán 8

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

A. Lí thuyết cần nhớ

- Tổng ba góc của một tam giác bằng ${180^0}$ ${180^0}$

- Lưu ý tính chất các trường hợp đồng dạng của tam giác.

- Định lí Pi – ta – go: Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

- Diện tích hình thang bằng tổng hai đáy nhân với chiều cao chia 2.

B. Bài tập ví dụ minh họa

Bài tập 1: Cho hình thang ABCD vuông tại A và D có hai đường chéo vuông góc với nhau tại I.

a. Chứng minh rằng: $\Delta AIB \sim \Delta DAB$ $\Delta AIB \sim \Delta DAB$

b. Chứng minh rằng: $\Delta AIB \sim \Delta IDC$ $\Delta AIB \sim \Delta IDC$

c. Cho AB = 4cm, CD = 9cm. Tính độ dài các cạnh DA, IA, IC.

d. Tính tỉ số diện tích: $\frac{{{S_{\Delta CDI}}}}{{{S_{\Delta ABI}}}}$ $\frac{{{S_{\Delta CDI}}}}{{{S_{\Delta ABI}}}}$

Hướng dẫn giải

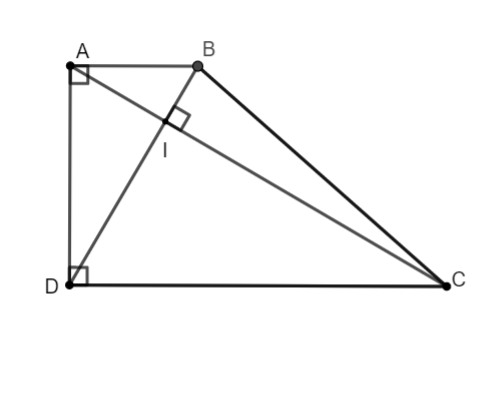
Cho hình thang ABCD vuông tại A và D

a. Xét hai tam giác $\Delta AIB$ $\Delta AIB$ và $\Delta DAB$ $\Delta DAB$ ta có:

$\widehat {DAB} = \widehat {AIB} = {90^0}$ $\widehat {DAB} = \widehat {AIB} = {90^0}$

$\widehat {ABI}$ $\widehat {ABI}$ chung

$\Rightarrow \Delta AIB \sim \Delta DAB$ $\Rightarrow \Delta AIB \sim \Delta DAB$

b. Xét hai tam giác $\Delta AIB$ $\Delta AIB$ và $\Delta IDC$ $\Delta IDC$ ta có:

$\widehat {DIC} = \widehat {AIB} = {90^0}$ $\widehat {DIC} = \widehat {AIB} = {90^0}$ (đối đỉnh)

Do ABCD là hình thang ⇒ AB //CD ⇒ $\widehat {BAI} = \widehat {ICD}$ $\widehat {BAI} = \widehat {ICD}$ (So le trong)

$\Rightarrow \Delta AIB \sim \Delta IDC$ $\Rightarrow \Delta AIB \sim \Delta IDC$

c. Ta có: $\Delta AIB \sim \Delta IDC \Rightarrow \frac{{IA}}{{IC}} = \frac{{IB}}{{ID}} = \frac{{AB}}{{CD}} = \frac{4}{9}$ $\Delta AIB \sim \Delta IDC \Rightarrow \frac{{IA}}{{IC}} = \frac{{IB}}{{ID}} = \frac{{AB}}{{CD}} = \frac{4}{9}$

$\Rightarrow \frac{{ID}}{{BD}} = \frac{9}{{13}}$ $\Rightarrow \frac{{ID}}{{BD}} = \frac{9}{{13}}$

Ta có: Tam giác ABD vuông tại A, AI vuông góc với BD $\Rightarrow A{D^2} = IA.BD = \frac{9}{{13}}D{B^2}$ $\Rightarrow A{D^2} = IA.BD = \frac{9}{{13}}D{B^2}$

$\begin{matrix} A{B^2} + A{D^2} = B{D^2} \Rightarrow A{B^2} + A{D^2} = \dfrac{{13}}{9}A{D^2} \hfill \\ \Rightarrow A{B^2} = \dfrac{4}{9}A{D^2} \Rightarrow AB = \dfrac{2}{3}AD \Rightarrow AD = \dfrac{3}{2}AB = 6\left( {cm} \right) \hfill \\ \Rightarrow AC = \sqrt {A{D^2} + D{C^2}} = 3\sqrt {13} \left( {cm} \right) \hfill \\ \end{matrix}$ $\begin{matrix} A{B^2} + A{D^2} = B{D^2} \Rightarrow A{B^2} + A{D^2} = \dfrac{{13}}{9}A{D^2} \hfill \\ \Rightarrow A{B^2} = \dfrac{4}{9}A{D^2} \Rightarrow AB = \dfrac{2}{3}AD \Rightarrow AD = \dfrac{3}{2}AB = 6\left( {cm} \right) \hfill \\ \Rightarrow AC = \sqrt {A{D^2} + D{C^2}} = 3\sqrt {13} \left( {cm} \right) \hfill \\ \end{matrix}$

Ta lại có: $\frac{{IA}}{{IC}} = \frac{4}{9} \Rightarrow IA = \frac{{12\sqrt {13} }}{{13}}\left( {cm} \right)$ $\frac{{IA}}{{IC}} = \frac{4}{9} \Rightarrow IA = \frac{{12\sqrt {13} }}{{13}}\left( {cm} \right)$

c. $\dfrac{{{S_{\Delta CDI}}}}{{{S_{\Delta ABI}}}} = \dfrac{{\frac{1}{2}.IC.ID}}{{\dfrac{1}{2}.IA.IB}} = \dfrac{{16}}{{81}}$ $\dfrac{{{S_{\Delta CDI}}}}{{{S_{\Delta ABI}}}} = \dfrac{{\frac{1}{2}.IC.ID}}{{\dfrac{1}{2}.IA.IB}} = \dfrac{{16}}{{81}}$

Bài tập 2: Cho hình thang vuông ABCD có $\widehat A = \widehat D = {90^0}$ $\widehat A = \widehat D = {90^0}$. I là trung điểm của AD, $\widehat {BIC} = {90^0}$ $\widehat {BIC} = {90^0}$. Chứng minh
a. $\Delta AIB{\text{ }} \sim \Delta DCI$ $\Delta AIB{\text{ }} \sim \Delta DCI$
b. $A{D^2} = 4AB.CD$ $A{D^2} = 4AB.CD$

Hướng dẫn giải

Cho hình thang ABCD vuông tại A và D

a. Xét hai tam giác $\Delta AIB{\text{ }}$ $\Delta AIB{\text{ }}$ và $\Delta DCI$ $\Delta DCI$ ta có:

$\widehat A = \widehat D = {90^0}$ $\widehat A = \widehat D = {90^0}$

Ta có: $\left\{ {\begin{array}{*{20}{c}} {\widehat {{I_1}} + \widehat {{B_1}} = {{90}^0}} \\ {\widehat {{I_3}} + \widehat {{C_2}} = {{90}^0}} \end{array}} \right.$ $\left\{ {\begin{array}{*{20}{c}} {\widehat {{I_1}} + \widehat {{B_1}} = {{90}^0}} \\ {\widehat {{I_3}} + \widehat {{C_2}} = {{90}^0}} \end{array}} \right.$ Mà $\widehat {{I_1}} + \widehat {{I_3}} = {90^0} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\widehat {{I_1}} = \widehat {{C_2}}} \\ {\widehat {{I_3}} = \widehat {{B_1}}} \end{array}} \right.$ $\widehat {{I_1}} + \widehat {{I_3}} = {90^0} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\widehat {{I_1}} = \widehat {{C_2}}} \\ {\widehat {{I_3}} = \widehat {{B_1}}} \end{array}} \right.$

$\Rightarrow \Delta AIB{\text{ }} \sim \Delta DCI$ $\Rightarrow \Delta AIB{\text{ }} \sim \Delta DCI$

b. Ta có:

$\begin{matrix} \Delta AIB{\text{ }} \sim \Delta DCI \Rightarrow \dfrac{{AB}}{{DI}} = \dfrac{{AI}}{{CD}} \Rightarrow AB.CD = AI.DI \Rightarrow AB.CD = \dfrac{1}{2}AD.\dfrac{1}{2}AD = \dfrac{1}{4}A{D^2} \hfill \\ \Rightarrow A{D^2} = 4.AB.DC \hfill \\ \end{matrix}$ $\begin{matrix} \Delta AIB{\text{ }} \sim \Delta DCI \Rightarrow \dfrac{{AB}}{{DI}} = \dfrac{{AI}}{{CD}} \Rightarrow AB.CD = AI.DI \Rightarrow AB.CD = \dfrac{1}{2}AD.\dfrac{1}{2}AD = \dfrac{1}{4}A{D^2} \hfill \\ \Rightarrow A{D^2} = 4.AB.DC \hfill \\ \end{matrix}$

C. Bài tập tự rèn luyện

Bài 1. Cho hình thang ABCD vuông tại A, đáy nhỏ AB, đường chéo BD vuông góc với BC. Chứng minh rằng:
a. $\widehat {ADB} = \widehat {BCD}$ $\widehat {ADB} = \widehat {BCD}$
b. ∆ADB ~ ∆BCD
c. $B{D^2} = AB.DC$ $B{D^2} = AB.DC$
Bài 2. Cho hình thang ABCD có đường chéo BD vuông góc với BC, biết $B{D^2} = AB.DC$ $B{D^2} = AB.DC$
Chứng minh rằng: Tứ giác ABCD là hình thang vuông.

Bài 3: Cho hình thang ABCD vuông tại A và D. Biết CD = 2AB = 2AD và $BC = a\sqrt 2$ $BC = a\sqrt 2$
a. Tính diện tích hình thang ABCD theo a
b. Gọi I là trung điểm BC, H là chân đường vuông góc từ D xuống AC. Chứng minh rằng:

Bài 4: Cho hình thang ABCD vuông góc tại A và D. Biết AB = AD = 3cm, BC = 6cm. Tính số đo của góc C.

Bài 5: Cho hình thang ABCD vuông tại A và D, có đường chéo DB vuông góc với cạnh bên BC tại B, biết AD= 3cm, AB= 4cm
a) Chứng minh: $\Delta ABD \sim \Delta BDC$ $\Delta ABD \sim \Delta BDC$
b) Tính độ dài cạnh DC
c) Gọi E là giao điểm của AC và BD. Tính diện tích tam giác AED.

Bài 6: Cho hình thang ABCD (BC là đáy nhỏ). Gọi I là trung điểm của CD. Qua I kẻ đường thẳng d // AB. Kẻ AH và BE vuông góc với d. Chứng minh tứ giác ABCD và tứ giác ABEH có diện tích bằng nhau.

---------------------------------------------------------------

Như vậy, VnDoc.com đã gửi tới các bạn Chứng minh hai tam giác đồng dạng. Ngoài ra, các em học sinh có thể tham khảo thêm các tài liệu khác do VnDoc sưu tầm và chọn lọc như Giải Toán 8, Giải Bài tập Toán 8, Chuyên đề Toán 8, để học tốt môn Toán hơn và chuẩn bị cho các bài thi đạt kết quả cao.

Chia sẻ, đánh giá bài viết

1.013