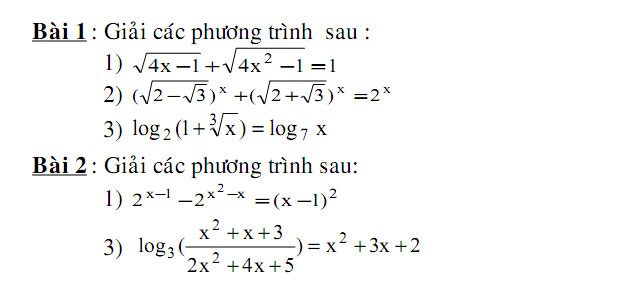Chuyên đề luyện thi vào Đại học - Ứng dụng tính đơn điệu của hàm số
Nhằm giúp các sĩ tử chuẩn bị tốt hơn cho kì thi vào đại học, cao đẳng sắp tới, VnDoc.com xin giới thiệu tới các bạn tài liệu luyện thi vào Đại học chuyên đề: Ứng dụng tính đơn điệu của hàm số. Tài liệu này tổng hợp lại các kiến thức cơ bản về tính đơn điệu của hàm số, đồng thời đưa ra các bài tập áp dụng, hy vọng sẽ giúp các bạn tự ôn luyện có hiệu quả.
ÔN THI ĐẠI HỌC CHUYÊN ĐỀ: ỨNG DỤNG TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
ỨNG DỤNG TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ ĐỂ
CHỨNG MINH BẤT ĐẲNG THỨC
GIẢI PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH – HỆ BẤT PHƯƠNG TRÌNH
********
Cơ sở để giải quyết vấn đề này là dùng đạo hàm để xét tính đơn điệu của hàm số dựa vào chiều biến thiên của hàm số để kết luận về nghiệm của phương trình, bất phương trình, hệ phương trình.
CÁC KIẾN THỨC CƠ BẢN
----------
I. Định nghĩa: Cho hàm số y = f(x) xác định trong khoảng (a,b).
![]()
II. Các tính chất
1) Tính chất 1: Giả sử hàm số y = f(x) tăng (hoặc giảm) trên khoảng (a,b) ta có:
|
f(u) = f(v) ↔ u = v (với u, v Є (a,b)) |
2) Tính chất 2: Giả sử hàm số y = f(x) tăng thêm trên khoảng (a,b) ta có:
|
f(u) < f(v) ↔ u < v (với u, v Є (a,b)) |
3) Tính chất 3: Giả sử hàm số y = f(x) giảm trên khoảng (a,b) ta có:
|
f(u) < f(v) ↔ u > v (với u, v Є (a,b)) |
4) Tính chất 4:
Nếu y = f(x) tăng trên (a,b) và y = g(x) là hàm hằng hoặc là một hàm số giảm trên (a,b) thì phương trình f(x) = g(x) có nhiều nhất một nghiệm thuộc khoảng (a,b)
* Dựa vào tính chất trên ta suy ra:
Nếu có x₀ Є (a,b) sao cho f(x₀) = g(x₀) thì phương trình f(x) = g(x) có nghiệm duy nhất trên (a,b)
BÀI TẬP ÁP DỤNG