Đề thi chọn học sinh giỏi lớp 12 THPT Lý Thái Tổ, Bắc Ninh năm 2014-2015

Đề thi học sinh giỏi lớp 12 có đáp án

Đề thi chọn học sinh giỏi lớp 12

Đề thi chọn học sinh giỏi lớp 12 THPT Lý Thái Tổ, Bắc Ninh năm 2014-2015 là tài liệu tổng hợp các đề thi trong kỳ thi chọn học sinh giỏi lớp 12 cấp trường THPT Lý Thái Tổ, tỉnh Bắc Ninh năm học 2014 - 2015 diễn ra ngày 14/9/2014. Chúng tôi xin giới thiệu tới bạn đọc bộ đề thi học sinh giỏi với các môn: Toán, Vật Lý, Hóa, Sinh, Lịch sử, Địa lý, Giáo dục công dân kèm hướng dẫn giải chi tiết.

Đề thi học sinh giỏi lớp 12 THPT Lý Thái Tổ tỉnh Bắc Ninh năm 2013 - 2014
Đề thi học sinh giỏi lớp 12 THPT tỉnh Hải Dương năm 2013 - 2014

Đề thi chọn học sinh giỏi lớp 12 môn Toán

SỞ GD & ĐT BẮC NINH
TRƯỜNG THPT LÝ THÁI TỔ

ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2014 – 2015
Môn thi: Toán – Lớp 12 – THPT
Thời gian làm bài: 150 phút (không kể thời gian phát đề)
Ngày thi: 14 tháng 09 năm 2014

Câu 1 (5.0 điểm)

Cho hàm số: (C_m) với m là tham số. Chứng minh rằng, với mọi m khác 0 đồ thị hàm số luôn cắt đường thẳng d: y = 3x - 3m tại hai điểm phân biệt A, B. Xác định m để đường thẳng d cắt các trục Ox, Oy lần lượt tại C, D sao cho diện tích tam giác OAB bằng 2 lần diện tích tam giác OCD.
Cho hàm số: y = x²(x² + a) với a là tham số. Chứng minh rằng, đồ thị hàm số đã cho có ba điểm cực trị tạo thành ba đỉnh của một tam giác nhọn khi và chỉ khi a < -2.

Câu 2 (5.0 điểm)

Giải phương trình: cosx + √3(sin2x + sinx) - 4cos2x cosx - cos² x + 2 = 0
Giải hệ phương trình:

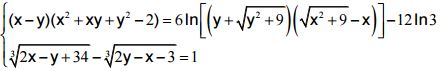
Câu 3 (3.0 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng có phương trình lần lượt là: d₁: x - 2y + 2 = 0, d₂: 3x - 3y + √6 = 0 và tam giác đều ABC có diện tích bằng √3 và trực tâm I thuộc d₁. Đường thẳng d₂ tiếp xúc với đường tròn nội tiếp tam giác ABC. Tìm tọa độ giao điểm của d₁ và đường tròn ngoại tiếp tam giác ABC biết điểm I có hoành độ dương.

Câu 4 (2.0 điểm) Cho hình chóp đều S.ABCD có cạnh bên bằng a, góc tạo bởi đường cao SH của hình chóp và mặt bên bằng φ. Tìm φ để thể tích khối chóp S.ABCD là lớn nhất biết a cố định, φ thay đổi.

Câu 5 (3.5 điểm)

Tính
Từ tập hợp tất cả các số tự nhiên có năm chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Tính xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau.

Câu 6 (1.5 điểm) Cho x, y, z là ba số thỏa mãn: x + y + z = xyz và x > 1, y > 1, z > 1. Tìm giá trị nhỏ nhất của biểu thức:

Tài liệu gồm đề thi học sinh giỏi của 7 môn: Toán, Vật Lý, Hóa, Sinh, Lịch sử, Địa lý, Giáo dục công dân. Các bạn có thể tải chi tiết từng môn trong bộ đề thi học sinh giỏi lớp 12 dưới đây: