Đề thi chọn học sinh giỏi lớp 12 tỉnh Vĩnh Phúc năm 2014-2015
Đề thi chọn học sinh giỏi lớp 12 môn Toán
Nhằm giúp các bạn học sinh lớp 12 có thêm tài liệu luyện đề, ôn tập và củng cố kiến thức môn Toán, Vndoc.com xin gửi đến các bạn đề thi chọn học sinh giỏi lớp 12 tỉnh Vĩnh Phúc năm 2014-2015. Đây là đề thi học sinh giỏi cấp tỉnh lớp 12 môn Toán, hi vọng sẽ giúp các bạn làm quen với các dạng câu hỏi thi học sinh giỏi, chuẩn bị sẵn sàng cho các kì thi sắp tới.
Tuyển tập đề thi học sinh giỏi tỉnh môn Toán lớp 12 từ năm 1999 - 2011
Khám phá cách giải một số bài toán hình học giải tích trong mặt phẳng
|
SỞ GIÁO DỤC-ĐÀO TẠO ĐỀ CHÍNH THỨC |
KÌ THI CHỌN HSG LỚP 12 THPT NĂM HỌC 2014-2015 Thời gian: 180 phút, không kể thời gian giao đề |
Câu 1 (2,5 điểm).
a) Tìm tham số m để hàm số y = x3 + 3mx2 +3(m+1)x + 2 nghịch biến trên một đoạn có độ dài lớn hơn 4.
b) Chứng minh rằng với mọi a, đường thẳng d: y = x + a luôn cắt đồ thị hàm số 
tại hai điểm phân biệt A,B. Gọi k1, k2 lần lượt là hệ số góc của các tiếp tuyến với (H) tại A và B. Tìm a để tổng k1 + k2 đạt giá trị lớn nhất.
Câu 2 (2,0 điểm).
a) Giải phương trình:
b) Có bao nhiêu số tự nhiên có ba chữ số 
thỏa mãn điều kiện a ≤ b ≤ c.
Câu 3 (1,5 điểm).
Giải hệ phương trình:
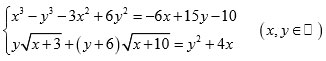
Câu 4 (1,5 điểm).
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có trung điểm của cạnh BC là điểm M (3;-1), đường thẳng chứa đường cao kẻ từ đỉnh B đi qua điểm E (-1;-3) và đường thẳng chứa cạnh AC đi qua điểm F (1;3). Tìm tọa độ các đỉnh của tam giác ABC, biết rằng điểm đối xứng của đỉnh A qua tâm đường tròn ngoại tiếp tam giác ABC là điểm D (4;-2) .
Câu 5 (1,5 điểm).
Cho hình chóp S.ABCD thỏa mãn SA = √5, SB = SC = SD = AB = BC = CD = DA = √3. Gọi M là trung điểm của cạnh BC. Tính thể tích khối chóp S.MCD và khoảng cách giữa hai đường thẳng SM,CD.
Câu 6 (1,0 điểm).
Cho các số thực a, b, c ≥ 1, thỏa mãn a + b + c = 6. Chứng minh rằng:
(a2 + 2)(b2 + 2)(c2 + 2) ≤ 216
