Đề thi học sinh giỏi lớp 9 THCS tỉnh Tiền Giang năm 2012 - 2013 môn Toán - Có đáp án

SỞ GIÁO DỤC VÀ ĐÀO TẠO TIỀN GIANG ĐỀ CHÍNH THỨC

KỲ THI CHỌN HSG LỚP 9 THCS CẤP TỈNH Năm học: 2012 - 2013 MÔN THI: TOÁN Thời gian làm bài: 150 phút (không kể thời gian giao đề) Ngày thi: 20/03/2012

Câu 1: (4,0 điểm)

1. Giải hệ phương trình: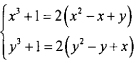

2. Cho phương trình x⁴ - 2mx² + 2m - 1 = 0 (1)

a. Tìm m để (1) có 4 nghiệm x₁, x₂, x₃, x₄ thỏa mãn:

b. Giải phương trình (1) với m vừa tìm được ở a.

Câu 2: (4,0 điểm)

Cho (P): y = x²; (d): y = x + m

Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt A, B sao cho: tam giác OAB là tam giác vuông

Câu 3: (4,0 điểm)

1. Cho 4 số a, b, c, d thỏa mãn điều kiện: a + b + c + d =

2. Chứng minh rằng: a² + b² + c² + d² ≥ 1

2. Cho m # -1 và a³ - 3a² + 3a(m + 1) - (m + 1)² = 0.

Hãy tìm giá trị nhỏ nhất (GTNN) của a.

Câu 4: (3,0 điểm)

Chứng minh rằng:

Câu 5: (5,0 điểm)

Cho tam giác ABC có các phân giác trong các góc nhọn BAC, ACB, CBA theo thứ tự cắt các cạnh đối tại các điểm M, P, N. Đặt a = BC, b = CA, c = AB; S_ΔMNP, S_ΔABC theo thứ tự là diện tích của tam giác MNP và tam giác ABC.

a. Chứng minh rằng:

b. Tìm giá trị lớn nhất (GTLN) của .