Đề thi học sinh giỏi môn Toán lớp 12 trường THPT Nguyễn Huệ, Phú Yên năm học 2016 - 2017

Đề thi học sinh giỏi môn Toán lớp 12

Đề thi học sinh giỏi môn Toán lớp 12 trường THPT Nguyễn Huệ, Phú Yên năm học 2016 - 2017 là tài liệu tham khảo hay được VnDoc.com sưu tầm và đăng tài. Hi vọng tài liệu này sẽ giúp cho quý thầy cô cùng các bạn học sinh lớp 12 đang trong quá trình ôn tập và củng cố lại kiến thức chuẩn bị có kì thi học sinh giỏi cấp trường môn Toán.

Đề thi học sinh giỏi cấp trường môn Toán lớp 12 trường THPT Hồng Lĩnh, Hà Tĩnh năm học 2016 - 2017

Đề thi chọn học sinh giỏi lớp 12 môn Toán tỉnh Bà Rịa - Vũng Tàu năm học 2015 - 2016

TRƯỜNG THPT NGUYỄN HUỆ Tổ: Toán

ĐỀ THI HỌC SINH GIỎI NĂM HỌC 2016-2017 MÔN: TOÁN - KHỐI 12 Thời gian 180 phút (không kể thời gian giao đề)

Câu 1: (4 điểm) Giải các phương trình sau:

Câu 2: (3 điểm) Cho hàm số , đồ thị (C) và đường thẳng (d_m): y = mx - 3 (với m ≠ 0 và m là tham số)
a) Chứng minh đồ thị (C) luôn cắt đường thẳng (d_m) tại hai điểm phân biệt A và B.

b) Tìm các giá trị của m để độ dài đoạn AB = √17.

Câu 3: (4 điểm)

a) Cho tam giác ABC có góc , AB = 3, AC = 4. Phân giác trong góc A cắt đường thẳng BC tại D. Tính độ dài AD?

b) Trong mặt phẳng Oxy, cho hình chữ nhật ABCD. Gọi M là trung điểm BC, M(3;1); H là hình chiếu của A lên BD, H(1/5;3/5); N là trung điểm của DH, đường thẳng AN có phương trình: x - 7y + 24 = 0. Tìm tọa độ các điểm A và D.

Câu 4: (4 điểm)

a) Giải phương trình: 2.cos4x - (√3 - 2)cos2x = sin2x + √3

b) Trong một hộp chứa 20 tấm thẻ, được đánh số từ 1 đến 20. Lấy ngẫu nhiên 3 tấm thẻ từ hộp. Tính xác suất để các số trên ba tấm thẻ lấy được có tổng là một số chia hết cho 3.

Câu 5: (3 điểm)

a) Giải phương trình:

b) Giải hệ phương trình: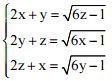

Câu 6: (2 điểm) Cho a, b, c là ba số thực dương thỏa mãn:

Tìm giá trị nhỏ nhất của biểu thức:

Đáp án đề thi học sinh giỏi môn Toán lớp 12