Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Hưng Yên (Lần 2)
Đề thi thử THPT Quốc gia năm 2016 môn Toán
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Hưng Yên (Lần 2) là đề thi thử Đại học hữu ích dành cho các bạn học sinh lớp 12, những bạn chuẩn bị bước vào kì thi THPT Quốc gia môn Toán. Mời các bạn tham khảo.
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Hưng Yên (Lần 1)
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đoàn Thượng, Hải Dương (Lần 2)
| TRƯỜNG THPT CHUYÊN HƯNG YÊN ———— |
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA NĂM 2016 Môn thi: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề |
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số ![]()
Câu 2 (1,0 điểm). Tìm các giá trị của m để hàm số y = x3 − 2x2 + mx − 2 đạt cực tiểu tại x = 2.
Câu 3 (1,0 điểm).
a) Tìm các căn bậc hai của số phức: ![]()
b) Giải phương trình: 4 log9 x + logx 3 = 3.
Câu 4 (1,0 điểm). Tính tích phân: ![]()
Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; 0; 3), B(−1; −2; 1) và C(−1; 0; 2). Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tính độ dài đường cao đỉnh A của tam giác đó.
Câu 6 (1,0 điểm).
a) Cho góc α thỏa mãn: π/4 < α < π/2 và tan α + cot α = 6. Tính A = cos 2α.
b) Trường THPT Chuyên Hưng Yên có 30 chi đoàn học sinh trong đó mỗi khối có 10 chi đoàn. Tổng kết tháng thanh niên 2016, Ban chấp hành đoàn trường đã chọn 4 bí thư các chi đoàn để tuyên dương. Giả sử việc chọn đó là ngẫu nhiên, tính xác suất để mỗi khối có ít nhất 1 bí thư được tuyên dương.
Câu 7 (1,0 điểm). Cho lăng trụ ABC.A'B'C' có độ dài cạnh bên bằng 2a, đáy ABC là tam giác vuông tại A, AB = a; AC = a√3 và hình chiếu vuông góc của A' trên mặt phẳng (ABC) là trung điểm của BC. Tính thể tích khối lăng trụ ABC.A'B'C' và khoảng cách giữa hai đường thẳng AA', B'C'.
Câu 8 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn tâm I(2; 2), điểm D là chân đường phân giác trong của góc BAC. Đường thẳng AD cắt đường tròn ngoại tiếp tam giác ABC tại điểm thứ hai M. Tính tọa độ các điểm A, B, C biết điểm J(0; 2) là tâm đường tròn ngoại tiếp tam giác ACD và phương trình đường thẳng CM: x − y + 4 = 0.
Câu 9 (1,0 điểm). Giải hệ phương trình:
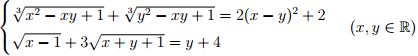
Câu 10 (1,0 điểm). Cho 2 số thực x, y thuộc khoảng (0; 1) và thỏa mãn điều kiện:
(x3 + y3)(x + y) − xy(x − 1)(y − 1) = 0.
Tìm giá trị lớn nhất của biểu thức: ![]()
————–Hết————–
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:..............................................................; Số báo danh:.................................


