Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Nguyễn Tất Thành, Yên Bái (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Nguyễn Tất Thành, Yên Bái (Lần 1) có 10 câu hỏi cùng đáp án đi kèm, là đề thi hữu ích dành cho các bạn học sinh lớp 12, những bạn chuẩn bị bước vào kì thi THPT Quốc gia, xét tuyển Đại học, Cao đẳng 2016. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Hạ Long, Quảng Ninh

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Lê Quý Đôn, Đà Nẵng

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Bến Tre

TRƯỜNG THPT CHUYÊN NGUYỄN TẤT THÀNH Tỉnh Yên Bái

ĐỀ THI THỬ KỲ THI THPT QUỐC GIA NĂM 2016 Môn Toán - Lần thứ 1 Thời gian làm bài: 180 phút, không kể thời gian giao đề.

Câu 1 (2,0 điểm). Cho hàm số x³ + 3x² + m (1)

1/ Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = -4.

2/ Xác định m để đồ thị của hàm số (1) có hai điểm cực trị A, B thỏa mãn tam giác OAB vuông tại O (O là gốc tọa độ).

Câu 2 (0,5 điểm). Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i.

Tìm mô đun của số phức

Câu 3 (0,5 điểm). Giải bất phương trình 1 + log_√2(x - 1) ≤ log₂(x² + x - 4).

Câu 4 (1,0 điểm). Tính tích phân

Câu 5 (1,0 điểm). Trong không gian với hệ toạ độ Oxyz, cho điểm I(-1;2;3) và mặt phẳng (P) có phương trình 4x + y - z - 1 = 0. Viết phương trình mặt cầu tâm I tiếp xúc với mặt phẳng (P) và tìm tọa độ tiếp điểm M.

Câu 6 (1,0 điểm).

a/ Cho góc α thỏa mãn cot = 2. Tính giá trị của biểu thức

b/ Xét tập hợp E gồm các số tự nhiên có 5 chữ số đôi một khác nhau tạo thành từ các chữ số {0; 1; 2; 3; 4; 5; 6; 7}. Chọn ngẫu nhiên một phần tử của tập hợp E. Tìm xác suất để phần tử chọn được là một số chia hết cho 5.

Câu 7 (1,0 điểm). Cho hình chóp S.ABC có AB = AC = a, , SA vuông góc với mặt phẳng (ABC), góc giữa hai mặt phẳng (SBC) và (ABC) là 60^o. Tính thể tích khối chóp S.ABC và khoảng cách từ trọng tâm G của tam giác ABC đến mặt phẳng (SBC) theo a.

Câu 8 (1,0 điểm).

Giải bất phương trình:

Câu 9 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có đỉnh B thuộc đường thẳng (d₁): 2x - y + 2 = 0, đỉnh C thuộc đường thẳng (d₂): x - y - 5 = 0. Gọi H là hình chiếu của B trên AC. Xác định tọa độ các đỉnh của hình chữ nhật ABCD biết M(9/5;2/5), K(9;2) lần lượt là trung điểm của AH, CD và điểm C có tung độ dương.

Câu 10 (1,0 điểm).

Cho 3 số thực không âm a, b, c thỏa mãn 5(a² = b² + c²) = 6(ab + bc + ca).

Tìm giá trị lớn nhất của biểu thức

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016

Câu 1:

1/ Khảo sát sự biến thiên và vẽ đồ thị

Với m = -4 ta có hàm số y = x3 + 3x2 - 4

Tập xác định: R

Sự biến thiên

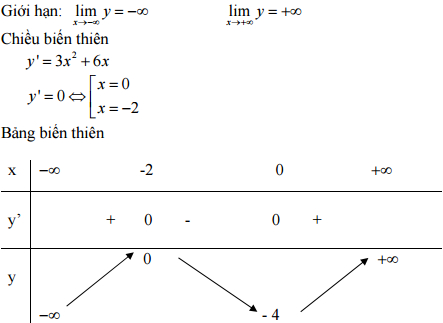
Hàm số đồng biến trên mỗi khoảng (-∞;-2) và (0;+∞)

Hàm số nghịch biến trên khoảng (-2; 0)

Cực trị:

Hàm số đạt cực đại tại x = -2, y_CĐ = 0

Hàm số đạt cực tiểu tại x = 0, y_CT = -4

Đồ thị:

Đồ thị cắt trục Ox tại điểm (-2; 0) và (1; 0)

Đồ thị cắt trục Oy tại điểm (0; -4)

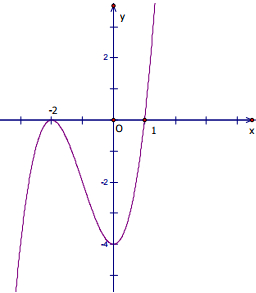
2/ Xác định m để đồ thị của hàm số (1) có hai điểm cực trị A, B thỏa mãn tam giác OAB vuông tại O (O là gốc tọa độ).

Câu 2

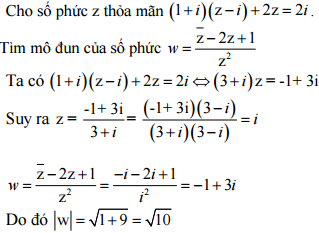
(Còn tiếp)