Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Đa Phúc, Hà Nội (Lần 3)
Đề thi thử THPT Quốc gia môn Toán năm 2016
Nhằm giúp các bạn học sinh luyện đề, thử sức trước kì thi Quốc gia, kì thi đại học sắp tới, VnDoc.com xin giới thiệu: Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Đa Phúc, Hà Nội (Lần 3). Đây là đề thi thử đại học 2016 có đáp án kèm theo. Mời các bạn cùng tham khảo.
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đa Phúc, Hà Nội (Lần 1)
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đa Phúc, Hà Nội (Lần 2)
TRƯỜNG THPT ĐA PHÚC ĐỀ THI THỬ LẦN 3 | ĐỀ THI THỬ THPT QUỐC GIA NĂM 2016 Môn thi: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề |
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số 
.
Câu 2 (1,0 điểm). Tìm các giá trị của m để đường thẳng d: y = x + m cắt đồ thị hàm số 
tại hai điểm phân biệt A và B sao cho trung điểm của AB nằm trên trục hoành.
Câu 3 (1,0 điểm).
a) Cho số phức z thoả mãn: (z - i)(1 - 2i) - 1 - 3i = 0. Tính môđun của số phức 
b) Giải phương trình: 24x-2.4-x+2 = 3.2x.
Câu 4 (1,0 điểm). Tính tích phân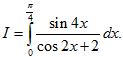 
Câu 5 (1,0 điểm). Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; 0; -3) và mặt phẳng (P): x + 2y - 2z - 12 = 0. Viết phương trình mặt cầu (S) có tâm thuộc trục Ox, đi qua A và tiếp xúc với (P).
Câu 6 (1,0 điểm).
a) Cho 
. Tính giá trị biểu thức 
b) Trong giải bóng đá của trường THPT X có 16 đội tham gia, trong đó có một đội của lớp Y và một đội của lớp Z. Ban tổ chức giải tiến hành bốc thăm ngẫu nhiên để chia thành hai bảng A và B, mỗi bảng 8 đội. Tính xác suất để hai đội Y và Z ở cùng một bảng.
Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi I là trung điểm của cạnh AB. Các mặt phẳng (SBD) và (SIC) cùng vuông góc với mặt đáy. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 600. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA và IC theo a.
Câu 8 (1,0 điểm). Trong mặt phẳng toạ độ Oxy, cho tam giác ABC vuông tại A. Gọi D là điểm đối xứng của A qua BC. Đường thẳng đi qua A vuông góc với CD có phương trình 4x - 3y + 20 = 0. Biết rằng phương trình đường thẳng AD: x - 2y + 10 = 0, điểm B nằm trên đường thẳng d: x + y - 5 = 0. Tìm toạ độ các điểm B, C.
Câu 9 (1,0 điểm). Giải hệ phương trình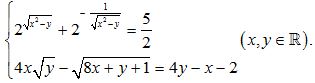 
Câu 10 (1,0 điểm). Cho các số thực dương a, b, c thoả mãn ab + bc + ca = 3abc. Tìm giá trị nhỏ nhất của biểu thức 
Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016
