Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đa Phúc, Hà Nội (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đa Phúc, Hà Nội (Lần 1) là đề thi thử đại học môn Toán có đáp án đi kèm. Đây là tài liệu ôn tập môn Toán hữu ích dành cho các bạn học sinh chuẩn bị bước vào kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng môn Toán.

Ôn thi Đại học môn Toán - Chuyên đề: Hình học giải tích trong không gian Oxyz

Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016

SỞ GD & ĐT HÀ NỘI TRƯỜNG THPT ĐA PHÚC ĐỀ THI THỬ LẦN 1

KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2016 Môn: TOÁN Thời gian: 180 phút

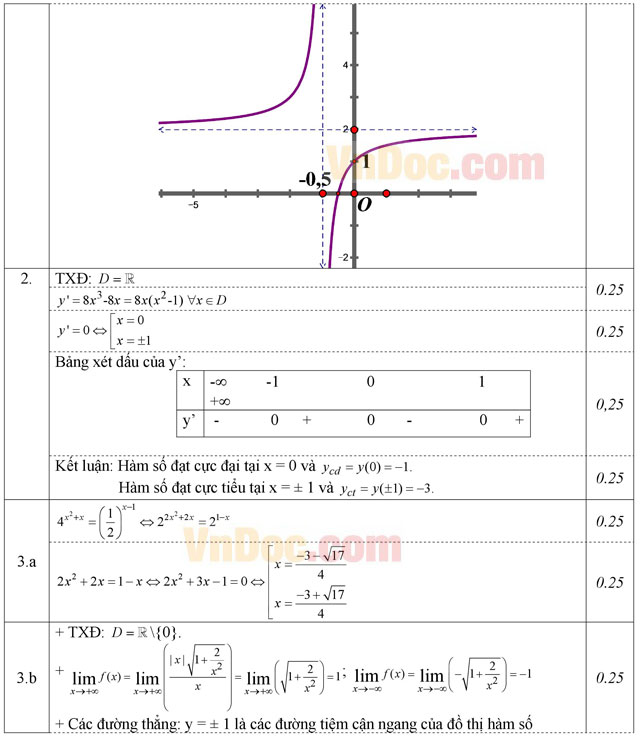
Câu 1: (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số .

Câu 2: (1,0 điểm). Tìm các điểm cực trị của hàm số y = 2x⁴ - 4x² - 1.

Câu 3: (1,0 điểm).

a) Giải phương trình trên tập số thực.

b) Tìm phương trình các đường tiệm cận đứng và ngang của đồ thị hàm số .

Câu 4: (1,0 điểm).

Tính diện tích hình phẳng giới hạn bởi đường cong y = (x - 1)lnx và đường thẳng y = x - 1.

Câu 5: (1,0 điểm).

Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;1) và mặt phẳng (P): 2x – y + 2z + 1 = 0. Viết phương trình mặt cầu tâm A tiếp xúc với mặt phẳng (P) và tìm tọa độ các giao điểm của mặt cầu đó với trục Ox.

Câu 6: (1,0 điểm).

a) Giải phương trình sin2x - √2sinx = 0.

b) Một đội văn nghệ gồm có 20 người trong đó có 12 nam và 8 nữ. Chọn ngẫu nhiên 8 người để hát đồng ca. Tính xác suất để 8 người được chọn có cả nam và nữ và số nữ nhiều hơn số nam.

Câu 7: (1,0 điểm). Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng a√3. Tính thể tích khối chóp S.ABC và diện tích của mặt cầu ngoại tiếp hình chóp S.ABC theo a.

Câu 8: (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang ABCD vuông tại B và C có AB > CD và CD = BC. Đường tròn đường kính AB có phương trình x² + y² – 4x – 5 = 0 cắt cạnh AD của hình thang tại điểm thứ hai N. Gọi M là hình chiếu vuông góc của D trên đường thẳng AB. Biết điểm N có tung độ dương và đường thẳng MN có phương trình 3x + y – 3 = 0, tìm tọa độ của các đỉnh A, B, C, D của hình thang ABCD.

Câu 9: (1,0 điểm). Giải bất phương trình trên tập số thực.

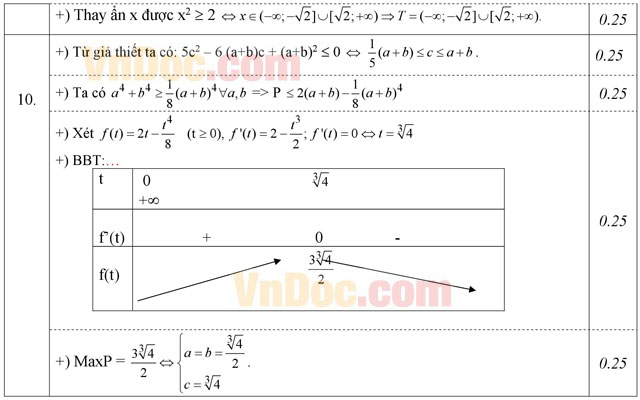
Câu 10: (1,0 điểm). Cho a, b, c là các số thực không âm thỏa mãn 8(a² + b² + c²) = 3(a + b + c)². Tìm giá trị lớn nhất của biểu thức P = a(1 – a³) + b(1 – b³) + c.

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán