Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Lý Thường Kiệt, Bình Thuận (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Lý Thường Kiệt, Bình Thuận (Lần 1) là đề thi thử đại học năm 2016 môn Toán có đáp án đi kèm. Đây là tài liệu ôn tập môn Toán hữu ích, giúp các bạn luyện tập và củng cố kiến thức môn Toán hiệu quả, từ đó bước vào kì thi THPT Quốc gia, luyện thi Đại học được tốt nhất.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Yên Thế, Bắc Giang (Lần 3)

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thuận Thành 1, Bắc Ninh (Lần 1)

SỞ GD&ĐT BÌNH THUẬN TRƯỜNG THPT LÝ THƯỜNG KIỆT TỔ TOÁN

ĐỀ THI THỬ LẦN I NĂM HỌC 2015-2016 MÔN: TOÁN Thời gian: 180 phút (không kể thời gian phát đề)

Bài 1 (2 điểm). Cho hàm số y = x⁴ – 2x² – 3 có đồ thị (C).

1. Khảo sát sự biến thiên và vẽ đồ thị (C) hàm số.
2. Dùng đồ thị (C) tìm m để phương trình x⁴ – 2x² + m = 0 có 4 nghiệm phân biệt.

Bài 2 (1 điểm). Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = xe^-x trên đoạn [0;3].

Bài 3 (1 điểm).

1. Giải phương trình 2^x - 2^1-x = 1.
2. Giải bất phương trình log₂ x - 1 > 2log₄(x - 1).

Bài 4 (1 điểm).

1. Cho cos2α = 2/3 (-π/4 < α < 0). Tính sin(α + π/4).
2. Xếp 6 học sinh trong đó có hai bạn A và B, ngồi vào một ghế dài đã được đánh số thứ tự từ 1 đến 6. Tính xác suất để hai bạn A và B được ngồi ở hai đầu của ghế (ở vị trí đánh số 1 và 6).

Bài 5 (1 điểm). Tính tích phân .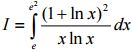

Bài 6 (1 điểm). Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh a, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Góc giữa SD và mặt đáy hình chóp bằng 45⁰. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AC, SD.

Bài 7 (1 điểm). Trong mp(Oxy) cho đường tròn (C) x² + y² – 2x + 4y = 0. Từ điểm M trên đường thẳng (d) x + y + 6 = 0, vẽ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC (B nằm trên đoạn MC) với đường tròn (C) sao cho tam giác ABC vuông tại B và có diện tích bằng 5. Tìm tọa độ của điểm M.

Bài 8 (1 điểm). Giải bất phương trình

Bài 9 (1 điểm). Cho 3 số thực âm a, b, c thỏa điều kiện a² + b² + c² ≤ 3. Tìm giá trị nhỏ nhất của biểu thức .

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán