Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Yên Thế, Bắc Giang (Lần 3)
Đề thi thử THPT Quốc gia năm 2016 môn Toán
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Yên Thế, Bắc Giang (Lần 3) được VnDoc.com sưu tầm và đăng tải, là tài liệu luyện tập hữu ích dành cho các bạn thí sinh chuẩn bị bước vào kì thi THPT Quốc gia, xét tuyển Đại học, Cao đẳng 2016. Mời các bạn cùng tham khảo.
Ôn thi Đại học môn Toán - Chuyên đề: Hệ phương trình đại số
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Phú Nhuận, TP. Hồ Chí Minh (Lần 1)
| TRƯỜNG THPT YÊN THẾ (Đề thi gồm 01 trang) | ĐỀ THI THỬ ĐẠI HỌC LẦN III LỚP 12 NĂM HỌC 2015 – 2016 Môn: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề |
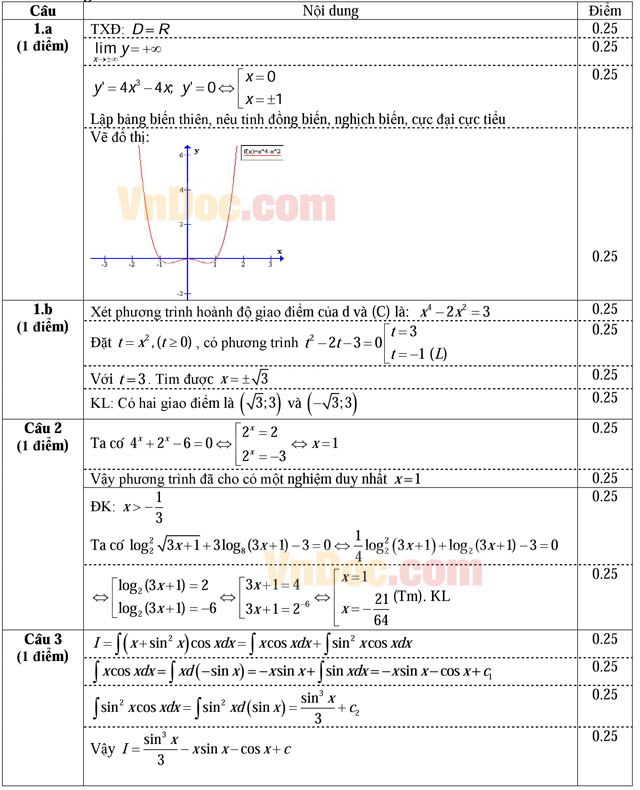
Câu 1 (2,0 điểm). Cho hàm số y = x4 - 2x2 (1).
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
b) Tìm toạ độ giao điểm của đồ thị (C) với đường thẳng d có phương trình y = 3.
Câu 2 (1,0 điểm). Giải các phương trình sau:
a) 4x + 2x = 6.
Câu 3 (1,0 điểm). Tính nguyên hàm: 
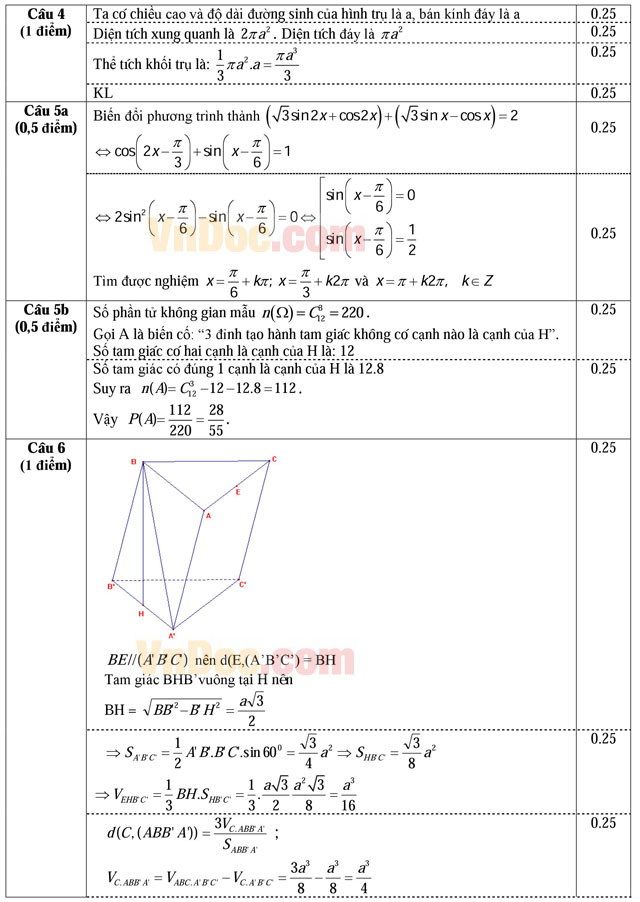
Câu 4 (1,0 điểm). Trong không gian cho hình vuông ABCD có cạnh bằng a. Tính diện tích xung quanh của hình trụ tròn xoay khi quay đường gấp khúc BCDA quanh trục là đường thẳng chứa cạnh AB và thể tích khối trụ đó.
Câu 5 (1,0 điểm).
a) Giải phương trình 3sin2x + cos2x + cosx = √3(sin2x + sinx).
b) Cho đa giác đều 12 đỉnh A1A2...A12 nội tiếp đường tròn (O). Chọn ngẫu nhiên 3 đỉnh của đa giác đó. Tính xác suất để 3 đỉnh được chọn tạo thành một tam giác không có cạnh nào là cạnh của đa giác đã cho.
Câu 6 (1,0 điểm). Cho hình lăng trụ tam giác ABC.A'B'C' có cạnh bên bằng a, đáy A'B'C' là tam giác đều cạnh bằng a, hình chiếu vuông góc của đỉnh B lên (A'B'C') là trung điểm H của cạnh A'B'. Gọi E là trung điểm của cạnh AC. Tính thể tích của khối tứ diện EHB'C'và khoảng cách từ điểm C đến mặt phẳng (ABB'A').
Câu 7 (1,0 điểm). Trong mặt phẳng với hệ toạ độ Oxy, cho hình vuông ABCD có đỉnh C(-4; -3) và M là một điểm nằm trên cạnh AB ( M không trùng với A và B). Gọi E, F lần lượt là hình chiếu vuông góc của A, C lên DM và I(2; 3) là giao điểm của CE và BF. Tìm toạ độ các đỉnh còn lại của hình vuông ABCD biết rằng đỉnh B nằm trên đường thẳng d có phương trình x - 2y + 10 = 0.
Câu 8 (1,0 điểm). Giải hệ phương trình: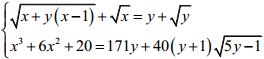 
trên tập số thực.
Câu 9 (1,0 điểm). Cho x, y, z là các số thực không âm thoả mãn điều kiện: x2 + y2 + z2 = 3. Tìm giá trị nhỏ nhất của biểu thức sau:
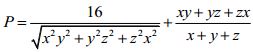
Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán
