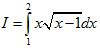Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Sơn La (Lần 1)

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Sơn La (Lần 1) được VnDoc.com sưu tầm và đăng tải. Đây là đề luyện thi THPT Quốc gia, ôn thi Đại học, Cao đẳng hữu ích dành cho các bạn thí sinh, giúp các bạn củng cố và nâng cao kỹ năng làm bài môn Toán. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thuận Châu, Sơn La (Lần 2)

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Sơn La (Lần 1)

Câu 1 (2 điểm).

1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số .
2. Viết phương trình tiếp tuyến với đồ thị (C) tại điểm có tung độ bằng 3.

Câu 2 (1 điểm)

1. Cho sinα = 3/5 và π/2 < α < π. Tính giá trị của biểu thức:
2. Cho số phức . Tìm |z|.

Câu 3 (1,5 điểm)

1. Giải bất phương trình sau:
2. Tính tích phân sau:

Câu 4 (1 điểm) Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AC = a√3, góc ABC = 60^o. Hình chiếu của đỉnh A' trên mặt phẳng (ABC) trùng với trung điểm H của cạnh BC, cạnh bên tạo với đáy góc 30^o. Tính thể tích khối lăng trụ và khoảng cách từ B' đến mặt phẳng (ACC'A').

Câu 5 (1 điểm) Trong không gian với hệ trục tọa độ Oxyz cho điểm A(-2; 1; 1) và mặt phẳng (α): 2x + 2y - z - 6 = 0. Viết phương trình mặt cầu tâm A và tiếp xúc với mặt phẳng (α). Tìm tọa độ tiếp điểm.

Câu 6 (1 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có N là trung điểm của BC và đường thẳng AN có phương trình 13x - 10y + 13 =0, điểm M(-1; 2) thuộc đoạn BD sao cho BD = 4DM. Gọi H là điểm thuộc tia NB sao cho NH = BC. Tìm tọa độ các đỉnh của hình bình hành biết 3BD = 2AD và H thuộc đường thẳng d: 2x - 3y = 0

Câu 7 (1,5 điểm)

1. Một công ty cần tuyển 3 nhân viên mới. Có 5 nam và 4 nữ nộp đơn dự tuyển. Giả sử khả năng trúng tuyển của mỗi người là như nhau. Tính xác suất để trong ba người được tuyển có ít nhất 2 nam.
2. Giải bất phương trình:

Câu 8 (1 điểm) Cho x, y, z là các số dương thỏa mãn: xyz = 8. Hãy tìm giá trị lớn nhất của biểu thức:

.....................................Hết.....................................