Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Sơn La (Lần 1)
Đề thi thử THPT Quốc gia năm 2016 môn Toán
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Sơn La (Lần 1) gồm 9 câu hỏi với độ khó tương đương đề thi chính thức từ Bộ GD&ĐT, đây là đề luyện thi THPT Quốc gia, xét tuyển Đại học, Cao đẳng 2016 hữu ích dành cho các bạn học sinh, mời các bạn tham khảo.
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Thanh Chương 1, Nghệ An
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Nguyễn Huệ, Hà Nội
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO SƠN LA TRƯỜNG THPT CHUYÊN ĐỀ THI CHÍNH THỨC |
ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2015 - 2016 (LẦN 1) Môn: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề |
Câu 1 (2,0 điểm). Cho hàm số: y = -x3 + 3x2 + 3(m2 - 1)x - 3m2 - 1 (1)
a) Khảo sát vẽ đồ thị hàm số khi m = 1.
b) Tìm m để hàm số (1) có hai điểm cực trị x1 và x2 đồng thời |x1 - x2| = 2.
Câu 2 (1,0 điểm). Giải các phương trình, bất phương trình sau:
a) 5x + 1 - 4 = 52x
b) log√5x - log5(x + 2) < log1/53
Câu 3 (1,0 điểm). Tính tích phân: 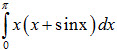
Câu 4 (1,0 điểm).
a) Giải phương trình: sin2x + √2cosx = 0.
b) Một lớp học có 28 học sinh trong đó có 15 học sinh nam và 13 học sinh nữ. Chọn ngẫu nhiên 5 học sinh tham gia Hội trại chào mừng ngày thành lập đoàn 26/3. Tính xác suât để trong 5 học sinh được chọn có ít nhất 3 học sinh nam.
Câu 5 (1,0 điểm). Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = a, BC = 2a. H là trung điểm cạnh AB, SH vuông góc với mặt phẳng đáy, cạnh bên SA = a5/2. Tính thể tích hình chóp S.ABCD và khoảng cách giữa hai đường thẳng HC và SD.
Câu 6 (1,0 điểm). Trong không gian Oxyz cho đường thẳng (d) và mặt phẳng (P) có phương trình:
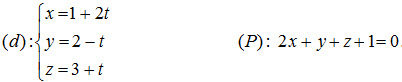
Tìm tọa độ điểm A là giao của đường thẳng (d) với (P). Viết phương trình đường thẳng qua A nằm trên mặt phẳng (P) và vuông góc với đường thẳng d.
Câu 7 (1,0 điểm). Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD; các điểm M, N và P lần lượt là trung điểm của AB, BC và CD; CM cắt DN tại điểm I(5;2). Biết P(11/2;11/2) và điểm A có hoành độ âm. Tìm tọa độ điểm A và D.
Câu 8 (1,0 điểm). Giải hệ phương trình: 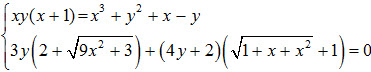
Câu 9 (1,0 điểm). Cho các số dương x, y, z thỏa mãn x > y; (x + z)(y + z) = 1.
Tìm giá trị nhỏ nhất của biểu thức: ![]()
Đáp án đề thi thử THPT Quốc gia 2016 môn Toán
Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 1
Câu 1.a:
Tập xác định: R
Sự biến thiên:
Giới hạn và tiệm cận
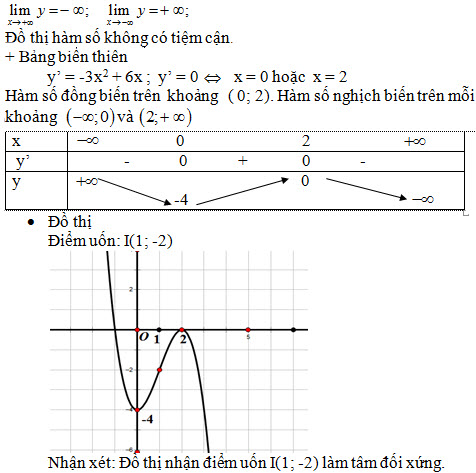
Câu 1.b:
y' = -3x2 + 6x + 3(m2 - 1)
Hàm số (1) có hai điểm cực trị khi y' = 0 có hai nghiệm phân biệt
Δ' = 9m2 > 0 ↔ m ≠ 0
|x1 - x2| = 2 ↔ (x1 + x2)2 - 4x1x2 = 4
Trong đó x1 + x2 = 2; x1x2 = 1 - m2
|x1 - x2| = 2
↔ 1 - m2 = 0
↔ m = ± 1 (TMĐK)
Vậy m m = ± 1