Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Nguyễn Huệ, Hà Nội (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Nguyễn Huệ, Hà Nội (Lần 1) gồm 10 câu hỏi có đáp án đi kèm, là tài liệu ôn tập môn Toán kì thi THPT Quốc gia 2016, mời các bạn tham khảo. Hy vọng tài liệu này sẽ giúp các bạn luyện tập và củng cố kiến thức hiệu quả.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Hàn Thuyên, Bắc Ninh (Lần 2)

Đề thi thử đánh giá năng lực ĐHQGHN 2016: Tư duy định lượng (môn Toán)

TRƯỜNG THPT CHUYÊN NGUYỄN HUỆ

ĐỀ KHẢO SÁT CHẤT LƯỢNG LẦN THỨ NHẤT NĂM HỌC 2015 – 2016 ĐỀ THI MÔN: TOÁN Thời gian làm bài: 180 phút

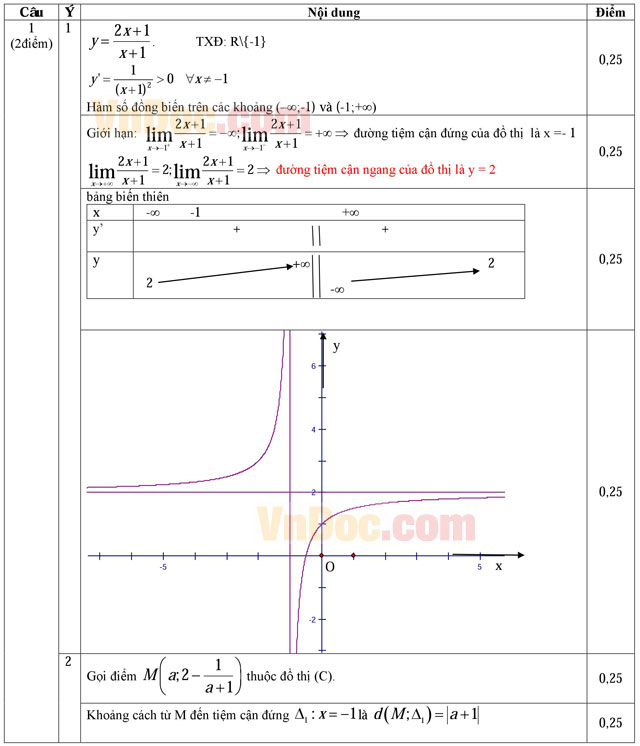
Câu 1 (2 điểm). Cho hàm số có đồ thị (C).

1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
2. Tìm trên đồ thị (C) điểm M sao cho tổng khoảng cách từ M đến hai đường tiệm cận của (C) là nhỏ nhất.

Câu 2 (1 điểm).

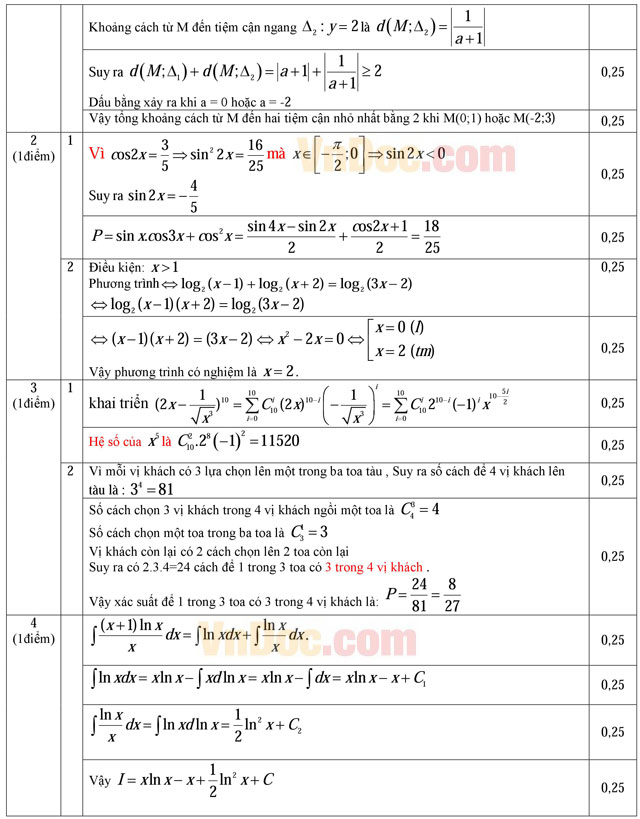
1. Tính giá trị của biểu thức P = sinx.cos3x + cos²x biết cos2x = 3/5, x ∈ (-π/2; 0).
2. Giải phương trình: log₈(x - 1)³ + log₂(x + 2) = 2log₄(3x - 2).

Câu 3 (1 điểm).

1. Tìm hệ số của x⁵ trong khai triển (với x > 0)
2. Một đoàn tàu có 3 toa chở khách đỗ ở sân ga. Biết rằng mỗi toa có ít nhất 4 chỗ trống. Có 4 vị khách từ sân ga lên tàu, mỗi người độc lập với nhau, chọn ngẫu nhiên một toa. Tính xác suất để 1 trong 3 toa có 3 trong 4 vị khách nói trên.

Câu 4 (1 điểm). Tìm nguyên hàm .

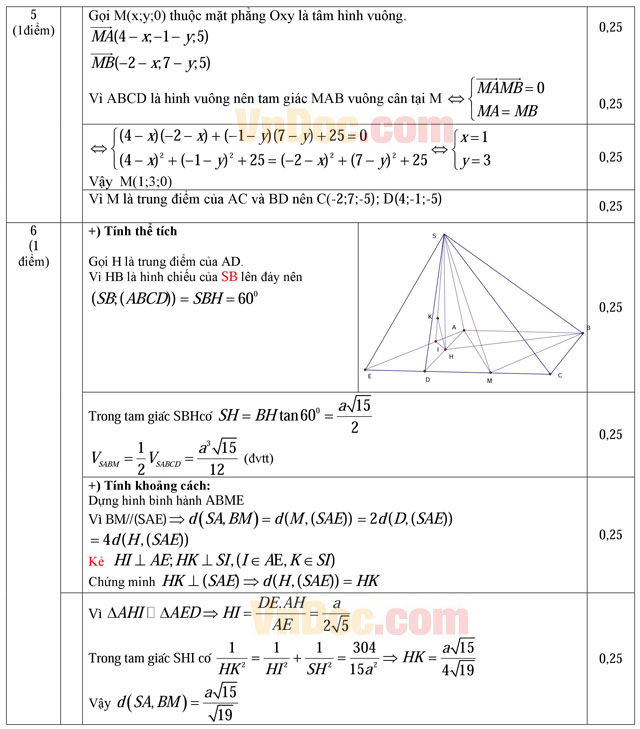
Câu 5 (1 điểm). Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có điểm A(4;-1;5) và điểm B(-2;7;5). Tìm tọa độ điểm C, D biết tâm hình vuông thuộc mp(Oxy).

Câu 6 (1 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu của S lên mặt phẳng (ABCD) là trung điểm của AD, góc giữa đường thẳng SB và mặt đáy bằng 60⁰. Gọi M là trung điểm của DC. Tính thể tích khối chóp S.ABM và khoảng cách giữa hai đường thẳng SA và BM.

Câu 7 (1 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có đỉnh A(-1;2), tâm đường tròn ngoại tiếp I(3/2;2), tâm đường tròn nội tiếp K(2,1). Tìm tọa độ đỉnh B biết x_B > 3.

Câu 8 (1 điểm). Giải bất phương trình .

Câu 9 (1 điểm). Cho x, y, z là các số không âm thỏa mãn x + y + z = 3/2. Tìm giá trị nhỏ nhất của P = x³ + y³ + z³ + x²y²z².

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán