Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Marie Curie
Đề thi thử THPT Quốc gia môn Toán trường THPT Marie Curie
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Marie Curie được chia sẻ bởi thầy Tài. Đề thi có 10 câu hỏi và đáp án đi kèm, đây là đề luyện thi THPT Quốc gia 2016 hữu ích dành cho các bạn học sinh lớp 12, những bạn chuẩn bị bước vào kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng 2016. Mời các bạn tham khảo.
Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016
TRƯỜNG THPT MARIE CURIE
ĐỀ THI THỬ THPT QUỐC GIA 2016
MÔN TOÁN
Thời gian làm bài: 180 phút
Câu 1. (2,0 điểm) Cho hàm số y = 2x3 + 6x2 - 4.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến song song với đường thẳng d: 15x - 2y = 0 và tiếp điểm có hoành độ dương.
Câu 2. (1,0 điểm)
a) Giải phương trình: (2sinx + 1)(3cos4x + 2sinx - 4) + 4cos2x = 3.
b) Tìm số phức z thỏa hệ thức: 
Câu 3. (0,5 điểm) Giải phương trình: log2(x + 2) + 2log4(x - 5) + log(1/2)8 = 0.
Câu 4. (1,0 điểm) Giải phương trình: 
Câu 5. (1,0 điểm) Tính tích phân: 
Câu 6. (1,0 điểm) Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB = BC = a và AD = 2a. Hình chiếu vuông góc của S trên đáy là trung điểm H của đoạn AB. Cạnh bên SC tạo với mặt đáy một góc bằng 60o. Tính theo a thể tích khối chóp S.ABCD và khoảng cách từ điểm H đến mặt phẳng (SCD).
Câu 7. (1,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy cho hình thang ABCD vuông tại A và B, có BC = 2AD, đỉnh A(-3;1) và trung điểm M của đoạn BC nằm trên đường thẳng d: x - 4y - 3 = 0. Tìm tọa độ các đỉnh còn lại của hình thang ABCD, biết H(6;-2) là hình chiếu vuông góc của B trên đường thẳng CD.
Câu 8. (1,0 điểm) Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và điểm A(5;4;-2). Tìm tọa độ điểm H trên đường thẳng
sao cho AH vuông góc với d và viết phương trình mặt cầu đi qua điểm A và có tâm là giao điểm của d với mặt phẳng Oxy.
Câu 9. (0,5 điểm) Gọi S là tập hợp các số tự nhiên gồm 4 chữ số khác nhau được chọn từ các số 0; 1; 2;3; 4; 5. Chọn ngẫu nhiên một số từ tập S, tính xác suất để số được chọn có mặt ít nhất chữ số 1 hoặc chữ số 2.
Câu 10. (1,0 điểm) Cho a , b , c là 3 số thực dương và thỏa 21ab + 2bc + 8ca ≤ 12.
Tìm giá trị nhỏ nhất của biểu thức: 
Đáp án đề thi thử THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Hà Nội - Amsterdam
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Lương Thế Vinh, Hà Nội
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Lương Thế Vinh, Đồng Nai
Câu 1:
1. a Học sinh tự làm
1. b Gọi M(x0;y0) là tiếp điểm (x0 > 0)
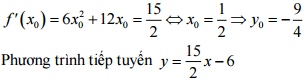
Câu 2:
2. a
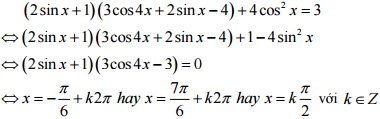
2. b
Giả sử z = x + yi với x, y ∈ R
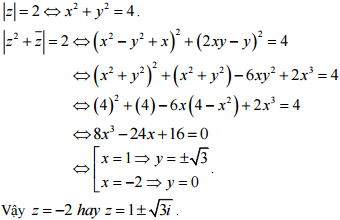
(Còn tiếp)
