Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Lương Thế Vinh, Đồng Nai (Lần 1)

Đề thi thử THPT Quốc gia 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Lương Thế Vinh, Đồng Nai (Lần 1) có 10 câu hỏi cùng đáp án đi kèm, đây là tài liệu ôn tập môn Toán hữu ích dành cho các bạn thí sinh chuẩn bị bước vào kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng 2016. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Hùng Vương, Gia Lai

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Anh Sơn 2, Nghệ An

Đề thi thử THPT Quốc gia năm 2016 môn Toán tỉnh Vĩnh Phúc

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỒNG NAI TRƯỜNG THPT CHUYÊN LƯƠNG THẾ VINH

THI THỬ QUỐC GIA LẦN 1 NĂM 2016 Môn: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số

Câu 2 (1 điểm). Tìm m để hàm số y = x³ - 3mx² + 3(m + 2)x + m - 1 có hai điểm cực trị.

Câu 3 (1,0 điểm).

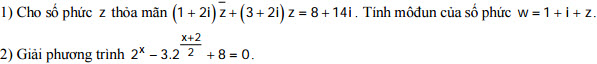
Câu 4 (1,0 điểm). Tính tích phân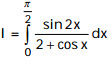

Câu 5 (1,0 điểm). Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng và điểm A(1;-4;1). Tìm tọa độ hình chiếu vuông góc của điểm A lên đường thẳng Δ và viết phương trình mặt cầu có tâm A và tiếp xúc với đường thẳng d.

Câu 6 (1,0 điểm).

Câu 7 (1,0 điểm). Cho hình lăng trụ đứng ABC.A'B'C' có tam giác ABC vuông tại A , AB = a, AC = a√3. Góc giữa đường thẳng A'C và mặt phẳng (ABC) bằng 30^o. Gọi N là trung điểm của cạnh BB'. Tính thể tích khối lăng trụ ABC.A'B'C' và tính cô sin của góc giữa hai đường thẳng AB và CN.

Câu 8 (1,0 điểm). Trong mặt phẳng Oxy , cho hình chữ nhật ABCD có AD = 2AB . Trên đoạn thẳng BD lấy điểm M sao cho DM = 4MB và gọi E, F lần lượt là trung điểm của các đoạn thẳng DM và BC. Tìm tọa độ các đỉnh A, B, C, D biết E(1;6), F(2;3), D có hoành độ lớn hơn 1 và A có hoành độ âm.

Câu 9 (1,0 điểm). Giải phương trình trên tập số thực: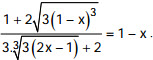

Câu 10 (1,0 điểm).

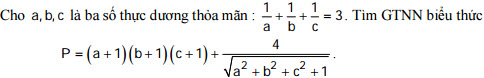
Đáp án đề thi thử THPT Quốc gia môn Toán

Câu 1:

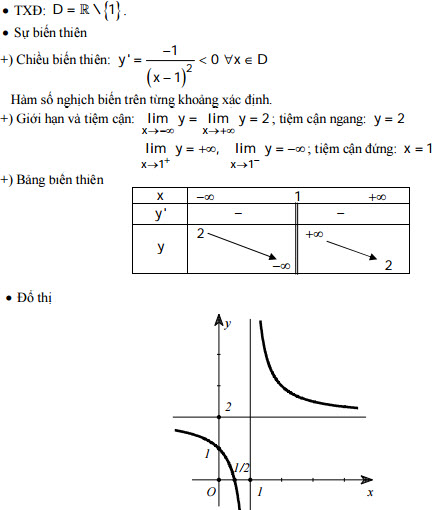
Câu 2:

TXĐ: D = R

Ta có y' = 3(x² - 2mx + m + 2), y' = 0 ↔ x² - 2mx + m + 2 = 0 (*)

Hàm số đã cho có hai điểm cực trị khi và chỉ khi (*) có hai nghiệm phân biệt, hay

Δ' = m2 - m - 2 > 0 ↔ m < - 1 hoặc m > 2

(Còn tiếp)