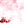Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2016 trường THPT Bố Hạ, Bắc Giang
Đề thi thử THPT Quốc gia 2016 môn Toán
Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2016 trường THPT Bố Hạ, Bắc Giang đáp án đi kèm được VnDoc.com sưu tầm và đăng tải. Đây là đề thi thử đại học năm 2016 hay, giúp các bạn học sinh luyện tập và củng cố kiến thức môn Toán, từ đó chuẩn bị cho các bài thi diễn ra hiệu quả.
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Thạch Thành 1, Thanh Hóa
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc
Tuyển tập các bài toán tích phân trong đề thi đại học từ 2002 - 2010
|
Trường THPT Bố Hạ Tổ Toán - Tin
|
ĐỀ THI THỬ THPT QUỐC GIA LẦN 2 NĂM HỌC 2015-2016 MÔN: TOÁN, LỚP 12 Thời gian làm bài: 150 phút, không kể thời gian phát đề |
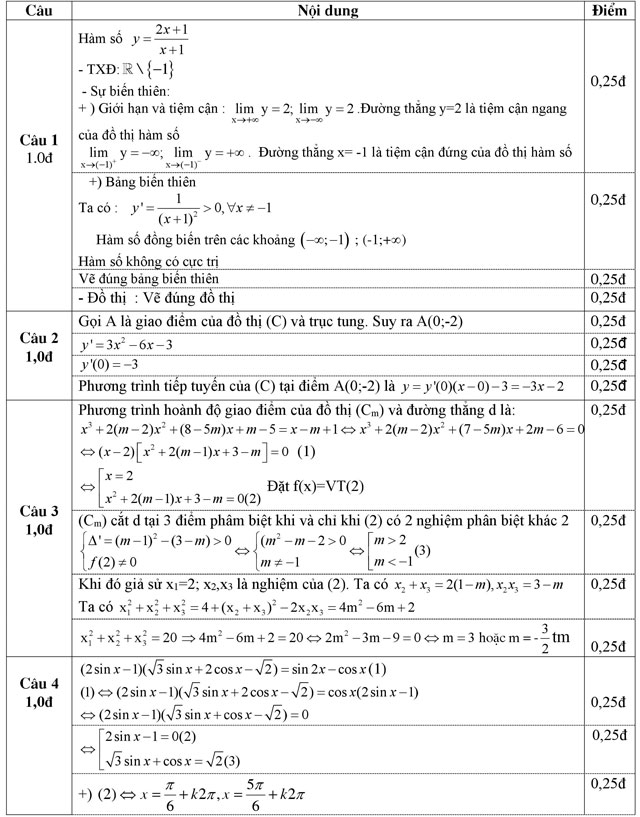
Câu 1 (1,0 điểm) Khảo sát sự biến thiên và vẽ đồ thi hàm số ![]() .
.
Câu 2 (1,0 điểm) Cho hàm số y = x3 - 3x2 - 3x + 2 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục tung.
Câu 3 (1,0 điểm) Cho hàm số y = x3 + 2(m - 2)x2 + (8 - 5m)x + m - 5 có đồ thị (Cm) và đường thẳng d: y = x - m + 1. Tìm m để d cắt (Cm) tại 3 điểm phân biệt có hoành độ tại x1, x2, x3 thỏa mãn: ![]() .
.
Câu 4 (1,0 điểm) Giải phương trình lượng giác: (2sinx - 1)(√3sinx + 2cosx - √2) = sin2x - cosx
Câu 5 (1,0 điểm)
a) Tìm số nguyên dương n thỏa mãn: A2n - 3C2n = 15 - 5n
b) Tìm hệ số của x8 trong khai triển ![]()
Câu 6 (1,0 điểm) Giải các phương trình sau:
a) 32+x + 32-x = 30
b) log2(x2 + x + 1) = log3(x + 3) + 1
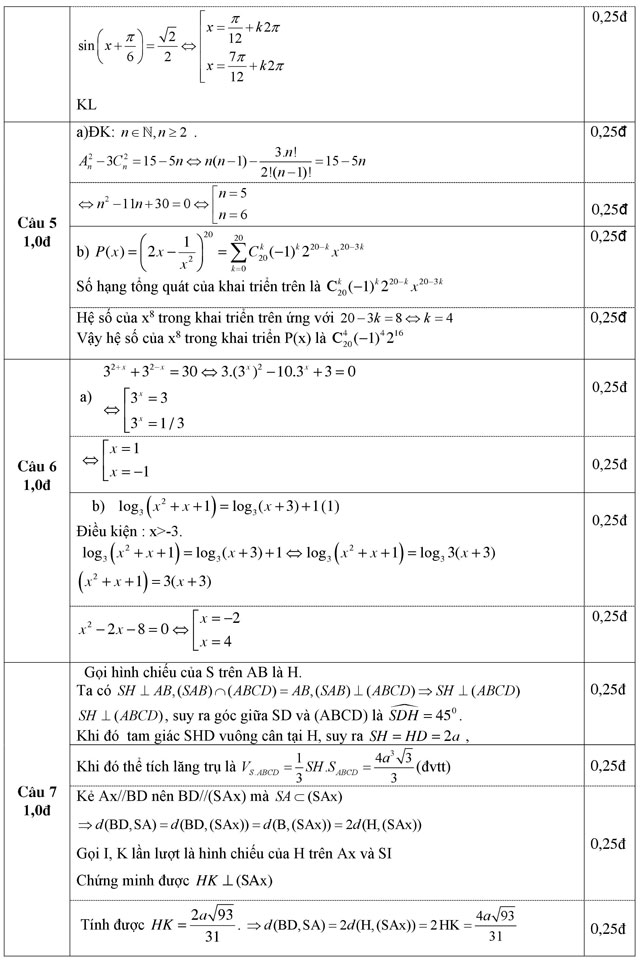
Câu 7 (1,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a√3. Mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Biết đường thẳng SD tạo với mặt đáy một góc 450. Tính thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA và BD.
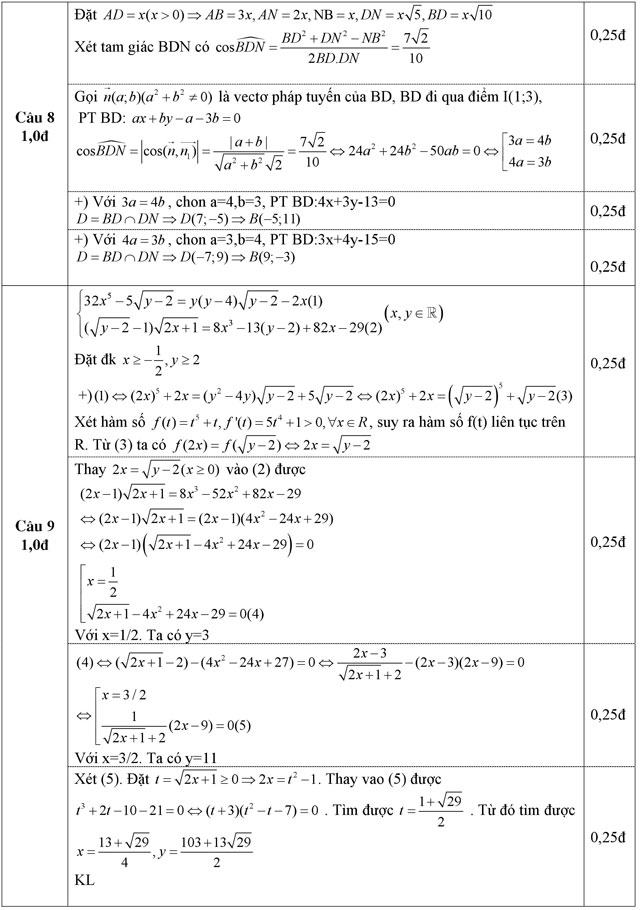
Câu 8 (1,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có tâm I(1;3). Gọi N là điểm thuộc cạnh AB sao cho AN = 2/3 AB. Biết đường thẳng DN có phương trình x + y - 2 = 0 và AB = 3AD. Tìm tọa độ điểm B.
Câu 9 (1,0 điểm) Giải hệ phương trình:
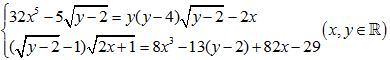
Câu 10 (1,0 điểm) Cho các số thực x, y, z thỏa mãn x > 2, y > 1, z > 0. Tìm giá trị lớn nhất của biểu thức:
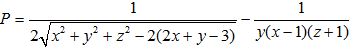
Đáp án đề thi thử THPT Quốc gia môn Toán