Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Hùng Vương, Gia Lai (Lần 1)

Đề thi thử THPT Quốc gia 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Hùng Vương, Gia Lai (Lần 1) được VnDoc.com sưu tầm và đăng tải, là tài liệu ôn thi THPT Quốc gia môn Toán hữu ích, giúp các bạn học sinh luyện tập và nâng cao kỹ năng làm bài, từ đó tự tin bước vào kì thi THPT Quốc gia 2016 đang tới gần.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Anh Sơn 2, Nghệ An

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Vĩnh Phúc

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Ngô Sĩ Liên, Bắc Giang

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = (2/3)x² - (1/3)x⁴

Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và nhỏ nhất của hàm số f(x) = (x - 2)e^x trên đoạn [0;2]

Câu 3 (1,0 điểm). Tính tích phân:

Câu 4 (1,0 điểm).

a) Giải phương trình log₂(x² + x) = log₅(3 - x).log₂5

b) Tính

Câu 5 (1,0 điểm). Trong không gian với hệ toạ độ Oxyz cho ba đường thẳng

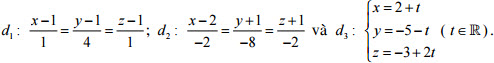
Xét vị trí tương đối của d₁ và d₂. Viết phương trình đường thẳng cắt trục oy và cắt cả ba đường thẳng d₁, d₂ và d₃.

Câu 6 (1,0 điểm).

a) Cho tam giác ABC có sinA, sinB, sinC theo thứ tự lập thành cấp số nhân và C - A = 60^o.Tính cos2B.

b) Gọi E là tập hợp các số tự nhiên gồm 3 chữ số khác nhau từng đôi một được chọn từ các số 0, 1, 2, 3, 4, 5. Chọn ngẫu nhiên ba số từ tập hợp E .Tính xác suất để trong ba số được chọn có đúng một số có mặt chữ số 4.

Câu 7 (1,0 điểm). Cho hình chóp S.ABC, có đáy là tam giác vuông cân tại A, AB = AC= a, trên cạnh BC lấy điểm H sao cho , SH vuông góc với mp(ABC), góc giữa SA và mặt phẳng (ABC) bằng 60^o. Tính theo a thể tích hình chóp S.ABC và khoảng cách giữa hai đường thẳng AB và SC.

Câu 8 (1,0 điểm). Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có B(1/2;3). Đường tròn tâm J nội tiếp tam giác ABC tiếp xúc với BC, AC, AB lần lượt tại M, N, P. Cho biết M (3;3) và đường thẳng đi qua hai điểm N, P có phương trình y  1 0 . Tìm tọa độ đỉnh A biết rằng A có tung độ âm.

Câu 9 (1,0 điểm). Giải hệ phương trình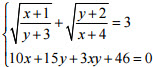

Câu 10 (1,0 điểm). Cho a, b, c là các số thực dương thỏa mãn a² + b² + c² = 17(a + b + c) - 2ab. Tìm giá trị nhỏ nhất của biểu thức

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016

Câu 1:

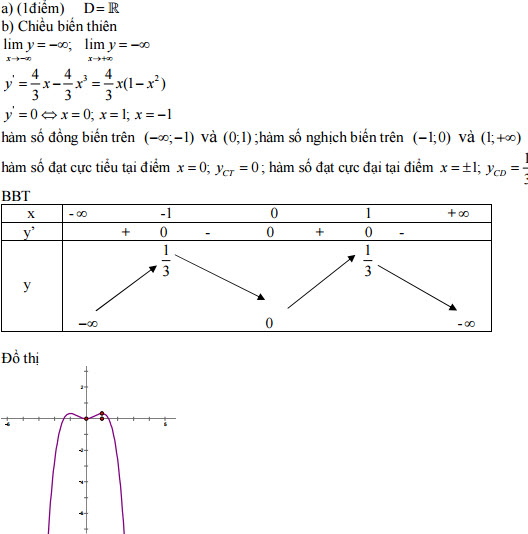
Câu 2:

Hàm số đã cho xác định và liên tục trên đoạn [0;2] và f'(x) = (x - 1)e^x

f'(x) = 0 ↔ x = 1 (thỏa mãn )

f(0) = -2, f(1) = -e, f(2) = 0

Vậy Giá trị lớn nhất của hàm số là 0 khi x = 2

Giá trị nhỏ nhất của hàm số là -e khi x = 1

(Còn tiếp)