Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Ngô Sĩ Liên, Bắc Giang (Lần 3)
Đề thi thử THPT Quốc gia năm 2016 môn Toán
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Ngô Sĩ Liên, Bắc Giang (Lần 3) là đề thi thử tốt nghiệp, đề thi thử dại học môn Toán năm 2016 có đáp án đi kèm. Hi vọng tài liệu này sẽ giúp các em học sinh lớp 12, các bạn thí sinh tự do ôn tập và củng cố kiến thức hiệu quả hơn, chuẩn bị sẵn sàng cho kỳ thi THPT Quốc gia 2016.
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Ngô Sĩ Liên, Bắc Giang
Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2016 trường THPT Ngô Sĩ Liên, Bắc Giang
| SỞ GD&ĐT BẮC GIANG TRƯỜNG THPT NGÔ SĨ LIÊN ———————- |
ĐỀ THI THỬ THPT QUỐC GIA LẦN 3 Môn: Toán 12 Thời gian: 120 phút, không kể thời gian phát đề |
Câu 1 (2,0 điểm). Cho hàm số ![]() (C) (với m là tham số thực).
(C) (với m là tham số thực).
- Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) với m = 1.
- Tìm m để đường thẳng d : y = x+ 2 cắt đồ thị hàm số (C) tại hai điểm A, B phân biệt.
Câu 2 (1,5 điểm).
- Giải phương trình: sinx + 2sin3x = −sin5x
- Giải phương trình: log3(x − 1)2 + log√3(2x − 1) = 2
Câu 3 (1,0 điểm). Tìm nguyên hàm sau: ![]()
Câu 4 (1,0 điểm). Trong không gian Oxyz, cho 4 điểm A(1; 1; 3), B(−2; 0; 4), C(2; −3; 5), D(0; 4; −5). Chứng minh rằng 4 điểm đã cho không đồng phẳng và tính thể tích của tứ diện ABCD.
Câu 5 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, AD = a√2. Hình chiếu vuông góc của đỉnh S lên (ABCD) trùng với trọng tâm của tam giác ABC, đường thẳng SD tạo với mặt đáy ABCD một góc 450. Tính thể tích của hình chóp S.ABCD và tính khoảng cách giữa hai đường thẳng SC và BD theo a.
Câu 6 (1,0 điểm). Để chuẩn bị cho Lễ kỷ niệm 70 năm thành lập của một trường THPT, nhà trường cần lập một đội tình nguyện viên gồm 40 em học sinh thông qua đơn đăng ký. Qua đăng ký có 150 em học sinh muốn tham gia đội tình nguyện viên, biết rằng trong 150 em đó có 60 em có học lực giỏi. Để đảm bảo công bằng nhà trường quyết định chọn ngẫu nhiên 40 học sinh từ 150 học sinh nói trên. Tính xác suất để trong số 40 em học sinh được chọn có đúng 80% học sinh có học lực giỏi.
Câu 7 (1,0 điểm). Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có AB = 2BC. Gọi H là hình chiếu của A lên đường thẳng BD. Gọi E, F lần lượt là trung điểm của các đoạn thẳng CD và BH. Biết điểm A(1; 1), phương trình đường thẳng EF : 3x − y − 10 = 0 và điểm E có tung độ âm. Tìm tọa độ các đỉnh B, C, D của hình chữ nhật.
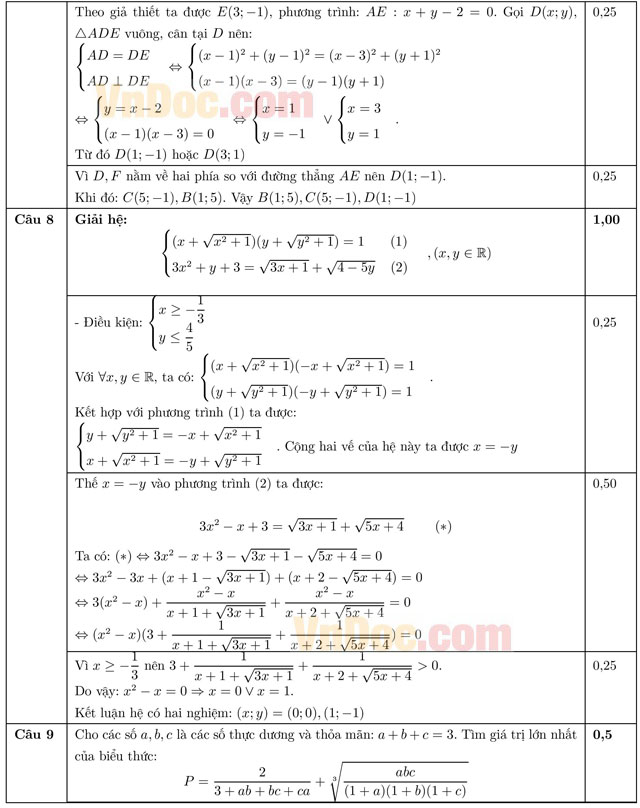
Câu 8 (1,0 điểm). Giải hệ phương trình sau:
![]()
Câu 9 (0,5 điểm). Cho các số a, b, c là các số thực dương và thỏa mãn: a + b + c = 3. Tìm giá trị lớn nhất của biểu thức:
![]()
Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán