Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Tam Dương, Vĩnh Phúc (Lần 4)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Tam Dương, Vĩnh Phúc (Lần 4) là đề thi thử THPT Quốc gia môn Toán hữu ích dành cho các bạn học sinh lớp 12, những bạn chuẩn bị bước vào kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng 2016 hiệu quả. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Bình Thuận

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Đại học Sư phạm Hà Nội (Lần 3)

TRƯỜNG THPT TAM DƯƠNG

KỲ THI CHUYÊN ĐỀ LẦN 4 NĂM HỌC 2015-2016 ĐỀ THI MÔN TOÁN 12 Thời gian làm bài: 180 phút, không kể thời gian giao đề

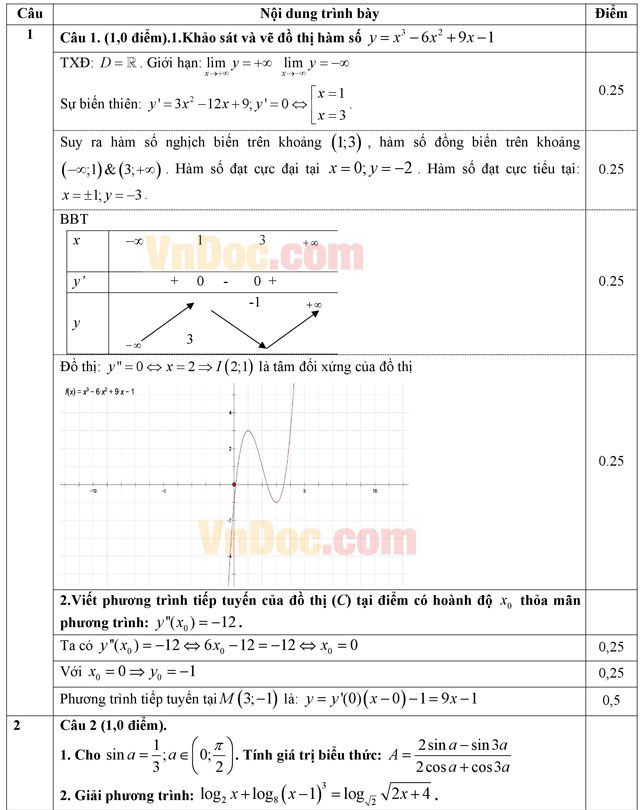
Câu 1 (2,0 điểm). Cho hàm số: y = x³ - 6x² + 9x - 1 (1).

1. Khảo sát và vẽ đồ thị (C) của hàm số (1).
2. Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x_o thỏa mãn phương trình: y''(x_o) = -12.

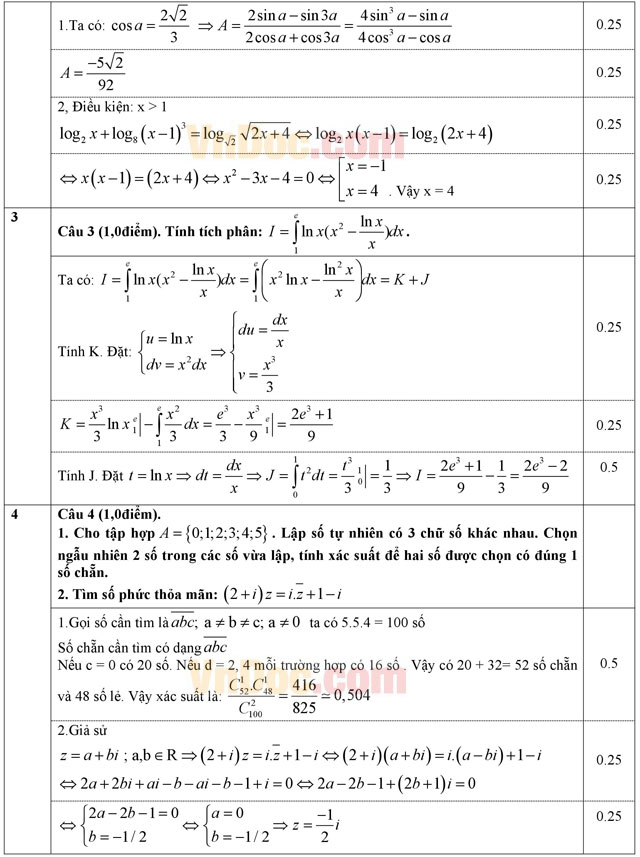
Câu 2 (1,0 điểm).

1. Cho . Tính giá trị biểu thức:
2. Giải phương trình: .

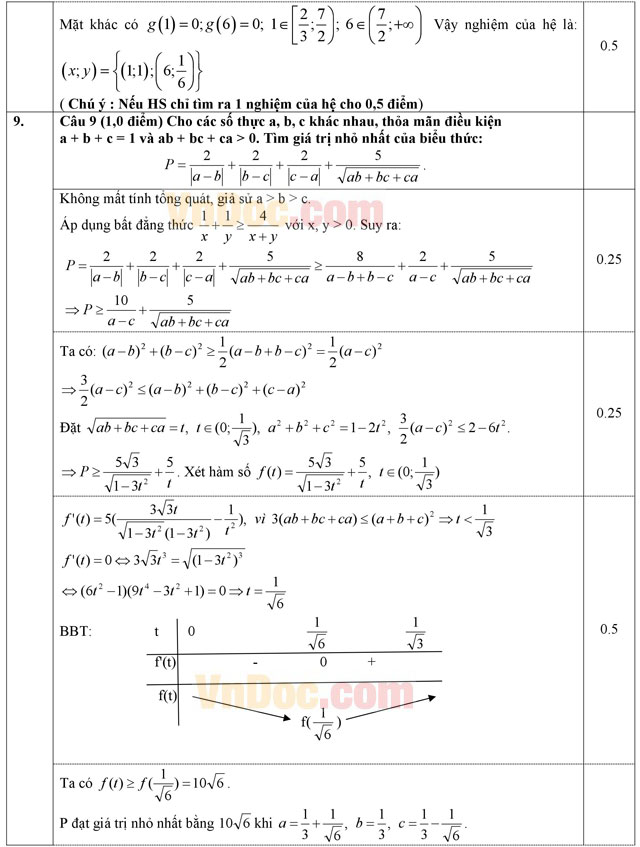
Câu 3 (1,0 điểm). Tính tích phân: .

Câu 4 (1,0 điểm).

1. Cho tập hợp A = {0; 1; 2; 3; 4; 5}. Lập số tự nhiên có 3 chữ số đôi một khác nhau. Chọn ngẫu nhiên 2 số trong các số vừa lập, tính xác suất để trong hai số được chọn có đúng 1 số chẵn.
2. Tìm số phức z thỏa mãn:

Câu 5 (1,0 điểm).

Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, AB = a, góc BAC = 120^o, AB' = 2a. Tính thể tích khối lăng trụ và khoảng cách giữa hai đường thẳng AB' và BC.

Câu 6 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC vuông tại A. Gọi H(5; 5) là hình chiếu của A lên BC, đường thẳng chứa đường phân giác trong góc A có phương trình x - 7y + 20 = 0. Đường thẳng chứa trung tuyến AM đi qua điểm K(10; -5). Tìm tọa độ các đỉnh A, B, C biết B có tung độ dương.

Câu 7 (1,0 điểm).

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1; 0; 1), B(2; 1; 2) và mặt phẳng (Q) có phương trình: x + 2y + 3z - 16 = 0.

1. Viết phương trình mặt phẳng (P) đi qua hai điểm A, B và vuông góc với mặt phẳng (Q).
2. Viết phương trình đường thẳng d nằm trong mặt phẳng (Q) đồng thời cắt đường thẳng AB và vuông góc với đường thẳng AB.

Câu 8 (1,0 điểm). Giải hệ phương trình: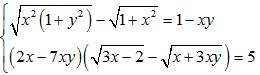

Câu 9 (1,0 điểm).

Cho các số thực a, b, c khác nhau, thỏa mãn điều kiện a + b + c = 1 và ab + bc + ca > 0. Tìm giá trị nhỏ nhất của biểu thức:

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán