Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đa Phúc, Hà Nội (Lần 2)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Nhằm giúp các bạn học sinh ôn thi tốt nghiệp, ôn thi THPT Quốc gia môn Toán, ôn thi đại học các khối A, B, D, VnDoc.com xin giới thiệu tới các bạn: Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đa Phúc, Hà Nội (Lần 2). Tài liệu này gồm đề thi đại học môn Toán có đáp án. Mời các bạn cùng tham khảo.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đa Phúc, Hà Nội (Lần 1)

Đề thi thử THPT Quốc gia môn Hóa học năm 2016 trường THPT Đa Phúc, Hà Nội (Lần 2)

Đề thi thử THPT Quốc gia năm 2016 môn Ngữ văn trường THPT Đa Phúc, Hà Nội (Lần 2)

Câu 1: (2,0 điểm).

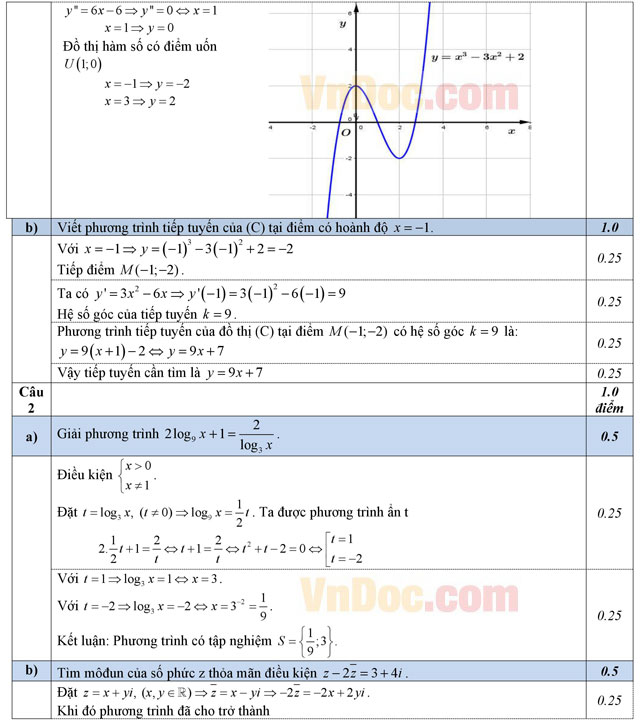
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x³ - 3x² + 2 (C).

b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x = -1.

Câu 2: (1,0 điểm).

a) Giải phương trình .

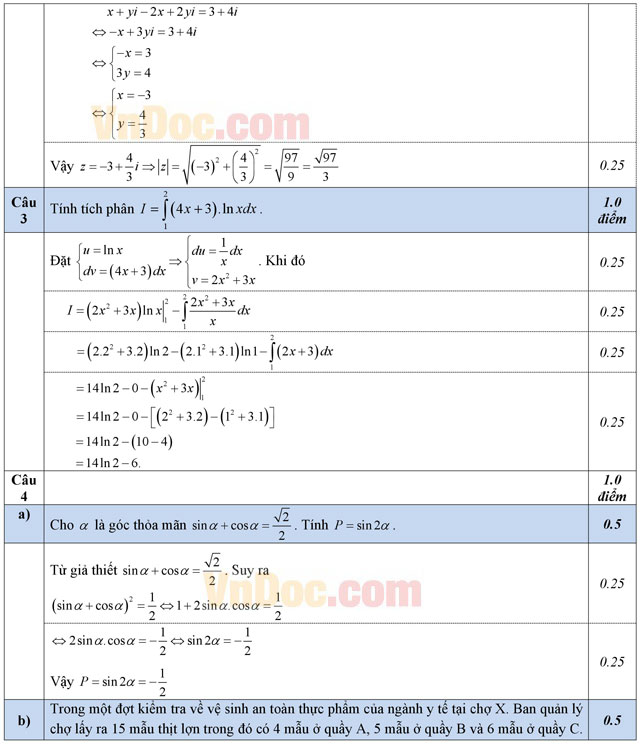
b) Tìm mô đun của số phức z thỏa mãn điều kiện .

Câu 3: (1,0 điểm). Tính tích phân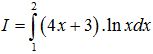

Câu 4: (1,0 điểm).

a) Cho là góc thỏa mãn sinα + cosα = √2/2. Tính P = 2sinα.

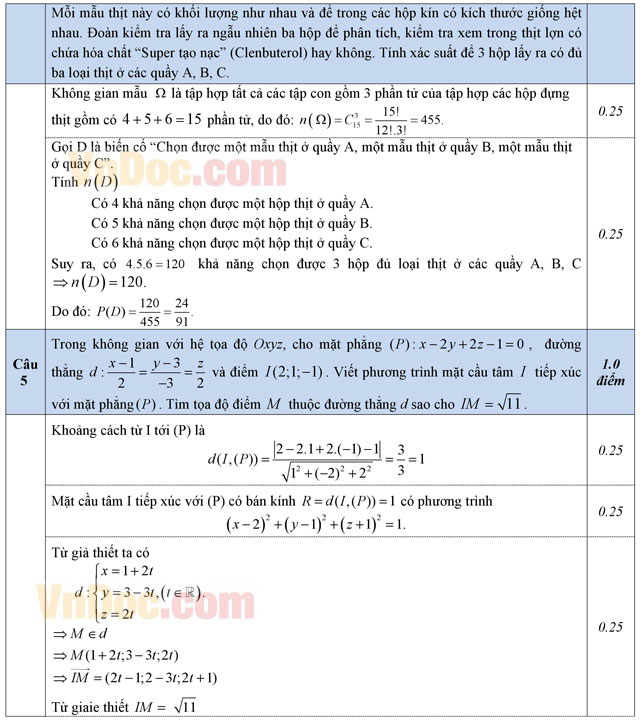
b) Trong một đợt kiểm tra về vệ sinh an toàn thực phẩm của ngành y tế tại chợ X. Ban quản lý chợ lấy ra 15 mẫu thịt lợn trong đó có 4 mẫu ở quầy A, 5 mẫu ở quầy B và 6 mẫu ở quầy C. Mỗi mẫu thịt này có khối lượng như nhau và để trong các hộp kín có kích thước giống hệt nhau. Đoàn kiểm tra lấy ra ngẫu nhiên ba hộp để phân tích, kiểm tra xem trong thịt lợn có chứa hóa chất "Super tạo nạc" (Clenbuterol) hay không. Tính xác suất để 3 hộp lấy ra có đủ ba loại thịt ở các quầy A, B, C.

Câu 5: (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - 2y + 2z - 1 = 0, đường thẳng và điểm I(2; 1; -1). Viết phương trình mặt cầu tâm tiếp xúc với mặt phẳng. Tìm tọa độ điểm thuộc đường thẳng d sao cho IM = √11.

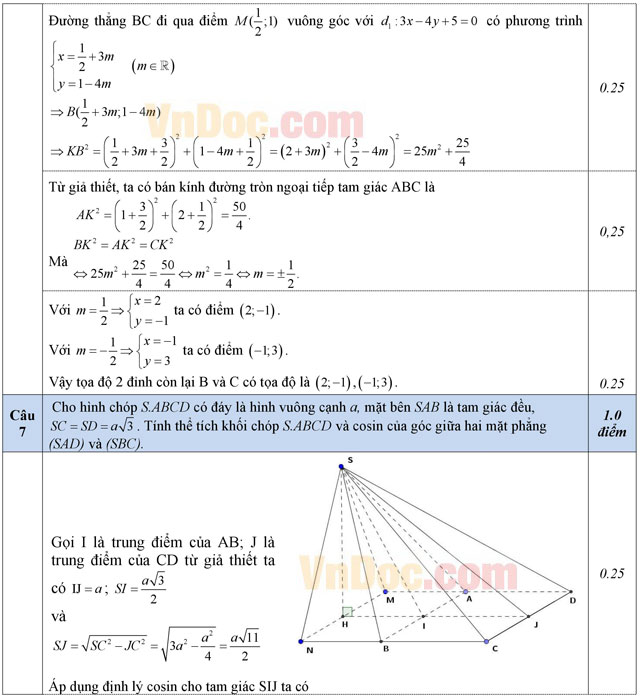
Câu 6: (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tâm đường tròn ngoại tiếp là điểm K(-3/2; -1/2), đường cao và đường trung tuyến kẻ từ đỉnh A lần lượt có phương trình là 3x - 4y + 5 = 0 và 2x - y = 0. Tìm tọa độ các đỉnh của tam giác ABC.

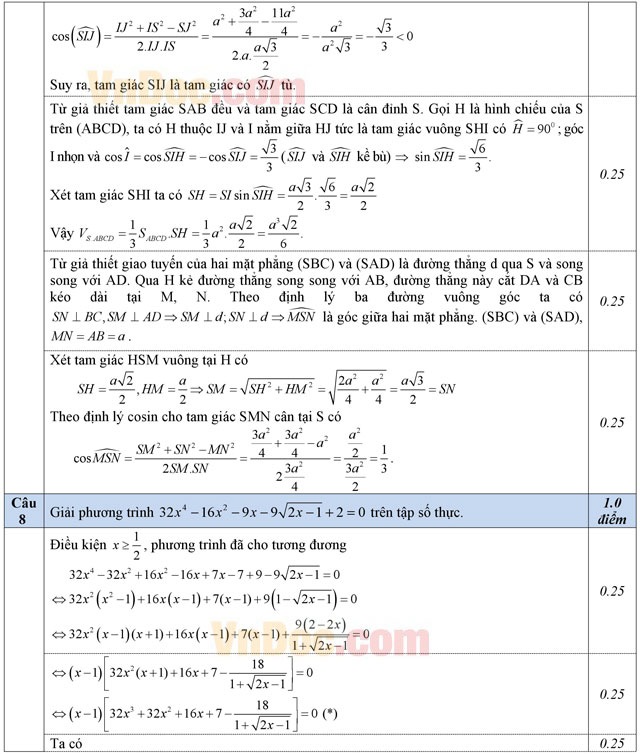
Câu 7: (1,0 điểm). Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều, SC = SD = a√3. Tính thể tích khối chóp S.ABCD và cosin của góc giữa hai mặt phẳng (SAD) và (SBC).

Câu 8: (1,0 điểm). Giải phương trình trên tập số thực.

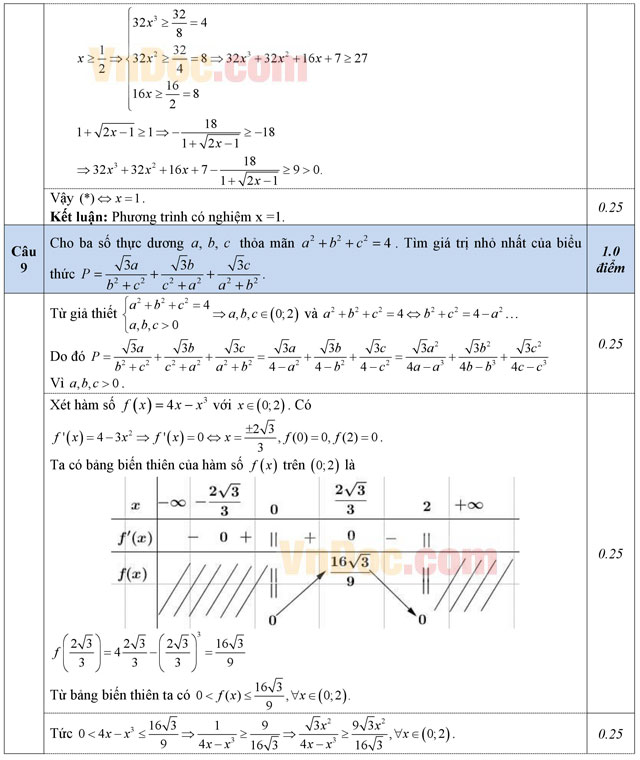
Câu 9: (1,0 điểm). Cho ba số thực dương a, b, c thỏa mãn a² + b² + c² = 4. Tìm giá trị nhỏ nhất của biểu thức .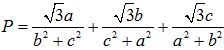

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán