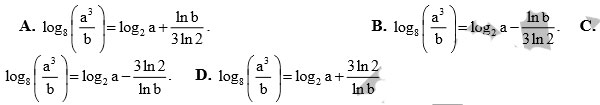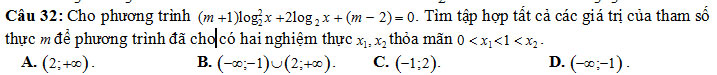Đề thi thử THPT quốc gia môn Toán năm 2018, sở GD&ĐT Hưng Yên
Đề thi thử THPT quốc gia môn Toán
VnDoc.com xin giới thiệu tới bạn đọc tài liệu: Đề thi thử THPT quốc gia môn Toán năm 2018, sở GD&ĐT Hưng Yên, tài liệu sẽ giúp các bạn học sinh rèn luyện giải nhanh các bài tập Toán một cách chính xác nhất. Mời các bạn và thầy cô tham khảo.
Đề thi thử THPT quốc gia môn Toán năm 2018, sở GD&ĐT Hưng Yên
Câu 1: Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu nào sau đây có tâm I (2; -1;1) và tiếp xúc với mặt phẳng (a): 2x + y - 2z - 7 = 0?
A. (x - 2)2 + ( y +1)2 + (z -1)2 = 4.
B. (x - 2)2 + ( y +1)2 + (z -1)2 = 36.
C. (x + 2)2 + ( y -1)2 + (z +1)2 = 4.
D. (x - 2)2 + ( y +1)2 + (z -1)2 = 2.
Câu 2: Với các số thực dương a, b bất kì, b  \(\ne\) 1. Mệnh đề nào dưới đây đúng?
\(\ne\) 1. Mệnh đề nào dưới đây đúng?
Câu 3: Tất cả các đường tiệm cận của đồ thị hàm số  \(y=\ \frac{\sqrt{x\ +\ 2}}{x^{2\ }-4}\) là:
\(y=\ \frac{\sqrt{x\ +\ 2}}{x^{2\ }-4}\) là:
A. y = 0, x = -2 và x = 2.
B. y = 0 và x = -2.
C. y = 0 và x = 2.
D. x = 2.
Câu 4: Để tìm diện tích S của hình phẳng giới hạn bởi đồ thị ( C ) 3 : y = x3, trục Ox và hai đường thẳng x = - 1; x = 2. Một học sinh thực hiện theo các bước như sau:

Lời giải của học sinh trên là đúng hay sai? Nếu lời giải sai thì sai từ bước nào?
A. Bước
B. Bước III
C. Bước I
D. Đúng
Câu 5: Biết f (x) là một nguyên hàm của hàm số  \(f\ \left(x\right)\ =\ \frac{1\ +\sqrt{x}}{\sqrt{x}}\) và f (1) = 2017. Tính f (4)
\(f\ \left(x\right)\ =\ \frac{1\ +\sqrt{x}}{\sqrt{x}}\) và f (1) = 2017. Tính f (4)
A. f (4) =2022.
B. f (4) = 4041.
C. f (4) = 2021.
D. f (4) = 2017.
Câu 6: Cho hình lăng trụ đứng ABC.A1B1C1 có đáy ABC là tam giác vuông, BA = BC = a. Gọi M là trung điểm của BC và khoảng cách giữa AM B1C bằng ![]() \(\frac{a\sqrt{7}}{7}\). Tính thể tích của khối lăng trụ ABC.A1B1C1 theo a.
\(\frac{a\sqrt{7}}{7}\). Tính thể tích của khối lăng trụ ABC.A1B1C1 theo a.
A.  \(\frac{a^{3^{^{\ ^{^{^{ }}}}}}\sqrt{2}}{2}\)
\(\frac{a^{3^{^{\ ^{^{^{ }}}}}}\sqrt{2}}{2}\)
B.  \(a^3\sqrt{2}\)
\(a^3\sqrt{2}\)
C.  \(\frac{a^3\sqrt{2}}{6}\)
\(\frac{a^3\sqrt{2}}{6}\)
D.  \(\frac{a^3\sqrt{2}}{4}\)
\(\frac{a^3\sqrt{2}}{4}\)
Câu 7: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x - y - 2z +1 = 0 và ba điểm A(1; -2; 0), B(1; 0; -1), C(0; 0; -2). Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng (P) và tiếp xúc với ba đường thẳng AB, AC, BC?
A. 1 mặt cầu.
B. Vô số mặt cầu.
C. 4 mặt cầu.
D. 2 mặt cầu.
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(4; 0; 0), B(a;b;0),C(0;0;c) (với a, b, c > 0) thỏa mãn độ dài đoạn AB = 2  \(\sqrt{10}\) góc ΣAOB = 450 và thể tích khối tứ diện OABC bằng 8. Tính tổng T = a + b + c.
\(\sqrt{10}\) góc ΣAOB = 450 và thể tích khối tứ diện OABC bằng 8. Tính tổng T = a + b + c.
A. T = 2
B. T = 10
C. T = 12
D. T = 14
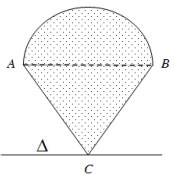
Câu 9: Cho hình phẳng (H) gồm nửa hình tròn đường kính AB và tam giác đều ABC (như hình vẽ). Gọi Δ là đường thẳng qua C và song song với AB. Biết AB =  \(2\sqrt{3}\) cm. Tính thể tích khối tròn xoay.
\(2\sqrt{3}\) cm. Tính thể tích khối tròn xoay.
A.  \(V\ =\ 3\sqrt{\pi\ +\ 9\pi^2\ cm^3}^{ }\)
\(V\ =\ 3\sqrt{\pi\ +\ 9\pi^2\ cm^3}^{ }\)
B.  \(V=8\sqrt{3\pi+\frac{9\pi^2}{2}}cm^3\)
\(V=8\sqrt{3\pi+\frac{9\pi^2}{2}}cm^3\)
C.  \(V\ =\ 16\sqrt{3}+9\pi^{2\ }cm^3\)
\(V\ =\ 16\sqrt{3}+9\pi^{2\ }cm^3\)
D.  \(V\ =\ 16\sqrt{3}+\frac{27\pi^2}{2}cm^3\)
\(V\ =\ 16\sqrt{3}+\frac{27\pi^2}{2}cm^3\)
Câu 10: Trong không gian với hệ tọa độ vuông góc Oxyz, cho mặt phẳng(P): x + 2y + z - 4 = 0, đường thẳng
 \(d:\ \frac{x+1}{2}\ =\ \frac{y}{1}\ =\ \frac{z\ +\ 2}{3}\) Tìm phương trình đường thẳng ∆ nằm trong mặt phẳng (P), đồng 2 1 3 thời cắt và vuông góc với đường thẳng d.
\(d:\ \frac{x+1}{2}\ =\ \frac{y}{1}\ =\ \frac{z\ +\ 2}{3}\) Tìm phương trình đường thẳng ∆ nằm trong mặt phẳng (P), đồng 2 1 3 thời cắt và vuông góc với đường thẳng d.
![]()
Câu 11: Cho số phức z thỏa mãn z = Ι4Ι . Biết tập các điểm biểu diễn số phức w = (3 + 4i)z + i là một đường tròn. Tìm bán kính r của đường tròn đó.
A. r = 20
B. r = 4
C. r = 25
D. r = 2
Câu 12: Rút gọn biểu thức  \(P\ =\ \frac{\left(a^{\sqrt{2}}\right)^{\sqrt{2}}}{a^{2+\sqrt{2}}\ .a^{2-\sqrt{2}}}^{ }\) 0 < a
\(P\ =\ \frac{\left(a^{\sqrt{2}}\right)^{\sqrt{2}}}{a^{2+\sqrt{2}}\ .a^{2-\sqrt{2}}}^{ }\) 0 < a  \(\ne\) 1) . Kết quả là:
\(\ne\) 1) . Kết quả là:
A.  \(P\ =\ \frac{1}{a^4}\)
\(P\ =\ \frac{1}{a^4}\)
B.  \(P\ =\ \frac{1}{a^2}\)
\(P\ =\ \frac{1}{a^2}\)
C.  \(P\ =\ \frac{1}{a^-}\)
\(P\ =\ \frac{1}{a^-}\)
D.  \(P\ =\ 1\)
\(P\ =\ 1\)
Câu 14: Một vật chuyển động với vận tốc thay đổi theo thời gian v(t) = 1- sin t (m / s). Quãng đường vật đi được trong khoảng thời gian từ thời điểm t = 0 (s) đến thời điểm  \(t\ =\ \frac{\pi}{2}\) (s) là:
\(t\ =\ \frac{\pi}{2}\) (s) là:
A.  \(\frac{\pi+1}{2}\ \left(m\right)\)
\(\frac{\pi+1}{2}\ \left(m\right)\)
B.  \(\frac{\pi}{2}\ +1\ \left(m\right)\)
\(\frac{\pi}{2}\ +1\ \left(m\right)\)
C.  \(\pi\ -\ 1\left(m\right)\)
\(\pi\ -\ 1\left(m\right)\)
D.  \(\frac{\pi}{2}-1\ \left(m\right)\)
\(\frac{\pi}{2}-1\ \left(m\right)\)
Câu 15: Cho hàm số y = f (x) liên tục trên ° và có đồ thị như hình vẽ dưới đây:
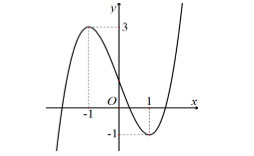
Khi đó phương trình  \(f\ \left(x-2\right)=\ \frac{1}{2}\) có bao nhiêu nghiệm?
\(f\ \left(x-2\right)=\ \frac{1}{2}\) có bao nhiêu nghiệm?
A. 2.
B. 0.
C. 6.
D. 4.
Câu 16: Tìm số thực m để đồ thị hàm số  \(y\ =\frac{9}{8}\ x^4\ +\ 3\left(m\ -\ 2017\right)x^2\ -2016\) có 3 điểm cực trị tạo thành một tam giác đều.
\(y\ =\frac{9}{8}\ x^4\ +\ 3\left(m\ -\ 2017\right)x^2\ -2016\) có 3 điểm cực trị tạo thành một tam giác đều.
A. m = 2015
B. m = -2017
C. m = 2017
D. m = 2016
Câu 18: Theo số liệu từ Tổng cục thống kê, dân số Việt Nam đầu năm 2017 là khoảng 95.414.640 người. Cho biết sự tăng dân số được ước tính theo công thức S = A.eNr (trong đó A: là dân số của năm lấy làm mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số hàng năm). Giả sử tỷ lệ tăng dân số hằng năm của Việt Nam trong giai đoạn 2015-2030 ở mức không đổi là 1,03%. Hỏi đến hết năm 2030 dân số Việt Nam khoảng bao nhiêu người?
A. 110.214.892 người.
B. 107.967.691 người.
C. 111.355.972 người.
D. 109.085.505 người.


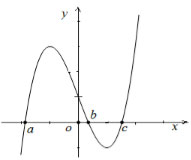
Chọn khẳng định đúng?
A. f (c) > f (b) > f (a).
B. f (b) > f (c) > f (a).
C. f (b) > f (a) > f (c).
D. f (c) > f (a) > f (b).
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị lớn nhất bằng – 2 và giá trị nhỏ nhất bằng 2.
B. Hàm số đạt cực đại tại x = -1 và đạt cực tiểu tại x = 1 .
C. Hàm số có giá trị cực tiểu là -1.
D. Đồ thị hàm số có điểm cực đại (1; 2) .
Câu 26: Gọi L, N lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số y = x3 - x2 -1 trên đoạn [0;2]. Tính L + N.
A. 2
B.  \(\frac{25}{21}\)
\(\frac{25}{21}\)
C.  \(\frac{11}{9}\)
\(\frac{11}{9}\)
D.  \(\frac{50}{27}\)
\(\frac{50}{27}\)
Câu 27: Cho hình chóp S.A BCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.CMN.
A.  \(R\ =\ \frac{a\sqrt{37}}{6}\)
\(R\ =\ \frac{a\sqrt{37}}{6}\)
B.  \(R\ =\ \frac{a\sqrt{29}}{8}\)
\(R\ =\ \frac{a\sqrt{29}}{8}\)
C. \(R=\ \frac{a\sqrt{93}}{12}\)
\(R=\ \frac{a\sqrt{93}}{12}\)
D.  \(R\ =\ \frac{5a\sqrt{3}}{12}\)
\(R\ =\ \frac{5a\sqrt{3}}{12}\)
Câu 28: Bạn A trúng tuyển vào trường đại học nhưng do không đủ tiền nộp học phí nên A quyết định vay ngân hàng trong 4 năm mỗi năm vay 8.000.000 đồng vào đầu năm học để nộp học phí theo hình thức lãi kép với lãi suất 3% /năm. Sau khi tốt nghiệp Đại học bạn A phải trả góp hàng tháng số tiền T (không đổi) cùng với lãi suất 0,3%/tháng trong vòng 3 năm vào ngày cuối tháng. Tính số tiền T hàng tháng mà bạn A phải trả cho ngân hàng (làm tròn đến kết quả hàng đơn vị).
A. 1.011.660 đồng.
B. 1.101.660 đồng.
C. 985.767 đồng.
D. 988.766 đồng.
Câu 29: Trong mặt phẳng phức, gọi A, B,C lần lượt là các điểm biểu diễn của các số phức z1 = -1+ 3i, z2 = 1+ 5i, z3 = 4 + i. Tìm số phức với điểm biểu diễn D sao cho tứ giác ABCD là một hình bình hành.
A. 2 - i
B. 3 + 2i
C. 2 + 3i
D. 3 + 5i
Câu 30: Cho hàm số  \(y\ =\ \frac{3x\ +1}{2x-1}\). Khẳng định nào dưới đây đúng?
\(y\ =\ \frac{3x\ +1}{2x-1}\). Khẳng định nào dưới đây đúng?
A. Đồ thị hàm số có tiệm cận ngang là  \(x\ =\ \frac{3}{2}\)
\(x\ =\ \frac{3}{2}\)
B. Đồ thị hàm số có tiệm cận đứng là  \(x\ =\frac{1}{2}\)
\(x\ =\frac{1}{2}\)
C. Đồ thị hàm số có tiệm cận đứng là  \(y\ =\ \frac{3}{2}\)
\(y\ =\ \frac{3}{2}\)
D. Đồ thị hàm số không có tiệm cận.
Câu 31: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1; 2;3), B(-4;1;1) , C(-9; 0; 2). Tìm tọa độ trọng tâm G của tam giác ABC.
A.  \(G\left(-\frac{2}{3};\ -1\ ;-\frac{2}{3}\right)\)
\(G\left(-\frac{2}{3};\ -1\ ;-\frac{2}{3}\right)\)
B. G(-4; 1; 2)
C.  \(G\left(-6;\ \frac{3}{2};\ 3\right)\)
\(G\left(-6;\ \frac{3}{2};\ 3\right)\)
D.  \(G\left(\frac{14}{3};\ \frac{1}{2};\ 0\right)\)
\(G\left(\frac{14}{3};\ \frac{1}{2};\ 0\right)\)
Câu 33: Hình nón đường sinh l , thiết diện qua trục của hình nón là tam giác vuông cân. Diện tích xung quanh của hình nón là.
A.  \(\frac{\pi l^2}{2\sqrt{2}}\)
\(\frac{\pi l^2}{2\sqrt{2}}\)
B.  \(\frac{\pi l^2}{2}\)
\(\frac{\pi l^2}{2}\)
C.  \(\frac{\pi l^2}{\sqrt{2}}\)
\(\frac{\pi l^2}{\sqrt{2}}\)
D.  \(\frac{\pi l^2}{4}\)
\(\frac{\pi l^2}{4}\)
Câu 34: Tính diện tích của hình cầu có bán kính R = 6 cm ?
A. 144 \(\pi\) cm2.
\(\pi\) cm2.
B. 36 \(\pi\)cm2.
\(\pi\)cm2.
C.24 \(\pi\)cm2.
\(\pi\)cm2.
D.288 \(\pi\)cm2.
\(\pi\)cm2.
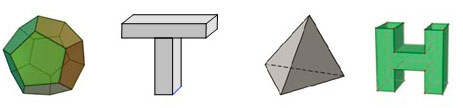
Câu 35: Trong các vật thể dưới đây.
Có bao nhiêu vật thể không phải là khối đa diện lồi ?
A. 1.
B. 4.
C. 3.
D. 2.
Câu 37: Trong không gian với hệ tọa độ Oxyz. Tìm tất cả các phương trình mặt phẳng đi qua điểm M (1; 2;3) và cắt tia Ox, trục Oy, tia Oz lần lượt tại các điểm A, B,C phân biệt sao cho 2OA = OB = 4OC.
A. 2x - 7 y + 4z = 0; 2x - y + 4z -12 = 0 .
B. 2x + y + 4z -16 = 0; 2x - y + 4z -12 = 0.
C. 2x + y + 4z -16 = 0; 2x + y + 4z -12 = 0 .
D. 2x + y + 4z -16 = 0; 2x - y - 4z +12 = 0.

Câu 40: Một ngôi biệt thự có 10 cây cột nhà hình trụ, tất cả đều có chiều cao bằng 4, 2 m. Trong đó, 4 cây cột trước đại sảnh có đường kính bằng 40 cm, 6 cây cột còn lại bên thân nhà có đường kính bằng 26cm. Chủ nhà dùng sơn để sơn 10 cây cột đó. Biết giá sơn là 380.000đ /m2 (kể cả phần thi công) thì người chủ phải trả bao nhiêu tiền để sơn 10 cây cột nhà trên (làm tròn đến đơn vị nghìn đồng)?
A. 14.647.000 đồng.
B. 13.627.000 đồng.
C. 15.844.000 đồng.
D. 16.459.000 đồng.
Câu 41: Có hai giá trị thực của m để đường thẳng d: y = -x+m cắt đồ thị (H) ![]() \(y\ =\ \frac{x-2}{x+1}\) tại hai điểm phân biệt ,AB sao cho
\(y\ =\ \frac{x-2}{x+1}\) tại hai điểm phân biệt ,AB sao cho \(\frac{1}{OA}\ +\ \frac{1}{OB}=\ 1\)với O là gốc tọa độ. Tìm tổng hai giá trị m trên.
\(\frac{1}{OA}\ +\ \frac{1}{OB}=\ 1\)với O là gốc tọa độ. Tìm tổng hai giá trị m trên.
A. -1.
B. 0.
C. 1.
D. 2.
Câu 42: Cho số phức z có phần ảo dương và thỏa mãn phức: z2 - 2z + 5 = 0. Tìm mô đun của số w = 4z - 5i
A.  \(\sqrt{41}\)
\(\sqrt{41}\)
B.  \(\sqrt{185}\)
\(\sqrt{185}\)
C. 5
D. 4
Câu 43: Cho hai số thực b và c (c>0). Kí hiệu A, B là hai điểm của mặt phẳng phức biểu diễn hai nghiệm phức của phương trình z2 + 2bz + c = 0. Trong mặt phẳng phức Oxy, tìm điều kiện của b và c để tam giác OAB là tam giác vuông.
A. c = 2b2.
B. b2 = c .
C. b = c .
D. b2 = 2c .
Câu 44: Một khách sạn có 100 phòng, hiện tại mỗi phòng cho thuê với giá 600 nghìn đồng một ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 40 nghìn đồng một ngày thì có thêm 5 phòng trống. Hỏi phải chọn giá phòng mới là bao nhiêu để thu nhập của khách sạn trong ngày là lớn nhất.
A. 800 nghìn.
B. 700 nghìn.
C. 750 nghìn.
D. 650 nghìn.
Câu 45: Cho hình lăng trụ tứ giác đều ABCD.A ' B 'C ' D ' có cạnh đáy bằng a và thể tích bằng  \(\frac{a^{3\sqrt{6}}}{2}\) Tính góc giữa mặt phẳng ( A' BD) với mặt đáy của lăng trụ đã cho.
\(\frac{a^{3\sqrt{6}}}{2}\) Tính góc giữa mặt phẳng ( A' BD) với mặt đáy của lăng trụ đã cho.
A. 60°
B. 30°
C. 45°
D. 135°
Câu 46: Trong không gian với hệ toạ độ Oxyz, cho điểm A(2;1; 4)và đường thẳng  \(\triangle\)
\(\triangle\)
x = 1 + t
y = 2 + t
z = 1 + 2t
Điểm H thuộc Δ có tọa độ bằng bao nhiêu thì độ dài đoạn AH nhỏ nhất?
A. H (-1; 0;-3).
B. H (3; 4;5).
C. H (0;1;-1).
D. H (2;3;3).
Câu 47: Tính thể tích V của khối tứ diện ABCD có độ dài các cạnh AB = CD = 5a, AC = BD = 6a và AD = BC = 7a.
A.  \(V\ =\ \frac{35\sqrt{2}}{2}a^3\)
\(V\ =\ \frac{35\sqrt{2}}{2}a^3\)
B.  \(V\ =\ 2\sqrt{105a^3}\)
\(V\ =\ 2\sqrt{105a^3}\)
C.  \(V\ =\ \frac{35}{2}a^3\)
\(V\ =\ \frac{35}{2}a^3\)
D.  \(V\ =\ 2\sqrt{95a^3}\)
\(V\ =\ 2\sqrt{95a^3}\)
Câu 48: Cho số phức z thỏa mãn điều kiện z + (2 + i)- z = 3 + 5i . Phần thực của số phức z là:
A. 2.
B. - 3.
C. 3.
D. - 2.
Câu 49: Trong không gian với hệ tọa độ Oxyz. Lập phương trình mặt phẳng (Q) đi qua điểm A (1; -2; -1) và vuông góc với đường thẳng  \(\triangle:\ \frac{x-1}{2}=\ \frac{y\ -\ 2}{-1}=\ \frac{z\ +\ 2}{1}\)
\(\triangle:\ \frac{x-1}{2}=\ \frac{y\ -\ 2}{-1}=\ \frac{z\ +\ 2}{1}\)
A. x + 2 y - 2z +1 = 0.
B. 2x - y + z - 3 = 0 .
C. 2x - y + z - 5 = 0.
D. 2x - y + z +1 = 0.

Đáp án đề thi thử THPT quốc gia môn Toán năm 2018
| Câu | Đáp án |
| 1 | A |
| 2 | B |
| 3 | B |
| 4 | C |
| 5 | A |
| 6 | A |
| 7 | C |
| 8 | D |
| 9 | C |
| 10 | A |
| 11 | A |
| 12 | B |
| 13 | C |
| 14 | D |
| 15 | C |
| 16 | D |
| 17 | C |
| 18 | A |
| 19 | B |
| 20 | C |
| 21 | B |
| 22 | B |
| 23 | D |
| 24 | A |
| 25 | B |
| 26 | D |
| 27 | C |
| 28 | A |
| 29 | A |
| 30 | B |
| 31 | B |
| 32 | C |
| 33 | C |
| 34 | A |
| 35 | D |
| 36 | C |
| 37 | B |
| 38 | B |
| 39 | B |
| 40 | C |
| 41 | D |
| 42 | C |
| 43 | A |
| 44 | B |
| 45 | A |
| 46 | D |
| 47 | D |
| 48 | A |
| 49 | B |
| 50 | C |