Đề thi thử THPT quốc gia môn Toán năm 2018, trường THPT Chuyên Nguyễn Đình Chiểu, Đồng Tháp

Đề thi thử THPT quốc gia môn Toán năm 2018

VnDoc.com xin giới thiệu tới các bạn học sinh tài liệu: Đề thi thử THPT quốc gia môn Toán năm 2018, trường THPT Chuyên Nguyễn Đình Chiểu, Đồng Tháp, bộ tài liệu bao gồm 50 câu hỏi trắc nghiệm kèm theo đáp án sẽ giúp các bạn học sinh rèn luyện cách giải các bài tập Toán một cách nhanh nhất. Mời các bạn học sinh và thầy cô tham khảo.

Đề thi thử THPT quốc gia môn Toán năm 2018, trường THPT Chuyên Nguyễn Đình Chiểu, Đồng Tháp

Câu 1. Hàm số nào sau đây đồng biến trên tập xác định của nó?

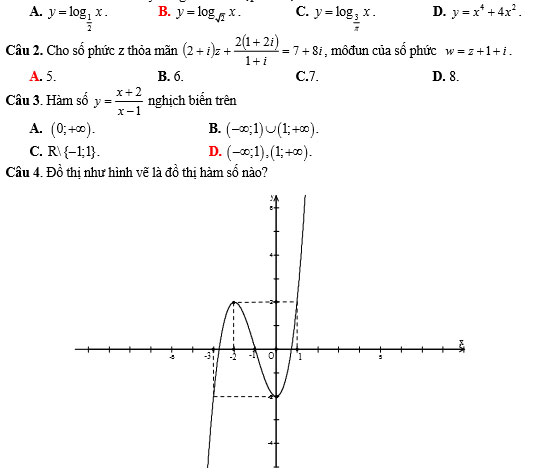
A. y = x³ + 3x² - 2

B. y = x³ - 3x² - 2

C. y = x³ + x - 2

D. y = -x³ - 3x² + 2

Câu 5. Giá trị cực tiểu y_CT của hàm số y = -x³ + 3x - 2016 là:

A. y_CT = -2014.

B. y_CT = -2016.

C. y_CT = -2018.

D. y_CT = -2020.

Câu 6. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y = \(\sqrt{4x-e^x}\), trục hoành và hai đường thẳng x = 1; x = 2. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục hoành.

A. V = 6 - e² + e.

B. V = 6 - e² - e.

C. V = \(\pi\)(6 - e² - e).

D. V = \(\pi\)(6 - e² + e).

A. \(-\frac{11}{8}\)

B. 0

C. -2

D. \(-\frac{5\sqrt{2}}{4}\)

Câu 11. Tìm m nhỏ nhất để hàm số y = x³ - 3mx² + x đồng biến trên R.

A. 1

B. \(\frac{1}{\sqrt{3}}\)

C. \(-\frac{1}{\sqrt{3}}\)

D. 2

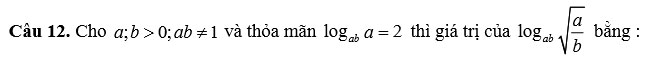
A. 1

B. \(\frac{3}{4}\)

C. 3

D. \(\frac{3}{2}\)

Câu 13. Số p = 2²⁰¹⁷ viết trong hệ thập phân, số đó có bao nhiêu chữ số?

A. 2016 chữ số.

B. 607 chữ số.

C. 608 chữ số.

D. 2017 chữ số.

Câu 14. Trong không gian Oxyz, cho 2 mặt phẳng (P) : x – y + 4z - 2 = 0 và (Q): 2x - 2z + 7 = 0. Góc giữa 2 mặt phẳng (P) và (Q) là:

A. 60⁰

B. 45⁰

C. 30⁰

D. 90⁰

Câu 15. Trong không gian Oxyz, cho mặt phẳng (a ) 3x – y + z - 4 = 0. mp (a ) cắt mặt cầu (S) tâm I(1;-3;3) theo giao tuyến là đường tròn tâm H(2;0;1), bán kính r = 2. Phương trình (S) là:

A. (x +1)² + ( y - 3)² + (z + 3)² = 18

B. (x -1)² + ( y + 3)² + (z - 3)² = 18

C. (x +1)² + ( y - 3)² + (z + 3)² = 4

D. (x -1)² + ( y + 3)² + (z - 3)² = 4

Câu 16. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Diện tích toàn phần của khối trụ là:

A. \(a^2\pi\sqrt{3}\)

B. \(\frac{27\pi a^2}{2}\)

C. \(\frac{a^2\pi\sqrt{3}}{2}\)

D. \(\frac{13a^{2\pi}}{6}\)

Câu 17. Trong không gian Oxyz, cho mặt cầu (S): x² + y² + z² - 2x + 4y - 2z - 3 = 0, đường thẳng \(\triangle\) : _{\(\frac{x}{2}=\ \frac{y+1}{-2}=\ z\)}

Mặt phẳng (P) vuông góc với D và tiếp xúc với (S) có phương trình là:

A. 2x - 2 y - 3 \(\sqrt{8}\)+ 6 = 0 và 2x - 2 y - 3\(\sqrt{8}\)- 6 = 0

B. 2x - 2 y + 3\(\sqrt{8}\) - 6 = 0 và 2x - 2 y - 3\(\sqrt{8}\) - 6 = 0

C. 2x - 2 y + z + 2 = 0 và 2x - 2 y + z -16 = 0

D. 2x + 2 y - z + 2 = 0 và 2x + 2 y - z -16 = 0

Câu 18. Hàm số F(x) = ax³ + bx² - 4x + 3 là một nguyên hàm của hàm số f ( x) = 3x² + 10x - 4. Khi đó b² - 8a bằng

A. -17

B.-39

C. 1

D. 17

Câu 19. Cho khối tứ diện OABC với OA,OB,OC vuông góc từng đôi một và OA = a, OB =2a, OC =3a. Gọi M, N lần lượt là trung điểm của hai cạnh AC, BC.Thể tích của khối tứ diện OCMN tính theo a bằng:

A. \(\frac{2a^3}{3}\)

B. \(a^3\)

C. \(\frac{3a^3}{4}\)

D. \(\frac{a^3}{4}\)

Câu 20. Cho khối tứ diện OABC với OA, OB, OC từng đôi một vuông góc và OA = OB = OC = 1. Bán kính mặt cầu ngoại tiếp tứ diên OABC bằng:

A. \(\frac{2}{3}\)

B. 1.

C. \(\frac{\sqrt{3}}{2}\)

D. \(\frac{1}{2}\)

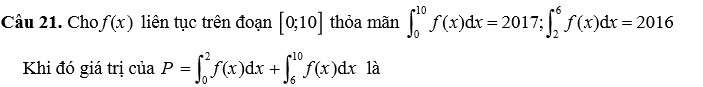
A. 1.

B. -1.

C. 3.

D. – 1.

Câu 22. Trong không gian với hệ trục Oxyz, mặt phẳng (P) đi qua hai điểm A (0;1;0), B (2;3;1) và vuông góc với mp (Q ) : x + 2y - z = 0 có phương trình là:

A. -4x - 3y + 2z + 3 = 0

B. 4x - 3y - 2z + 3 = 0

C. 2x - 3 y + z + 3 = 0

D. -4x + 5 y - 2z - 5 = 0

Câu 23. Biết rằng đồ thị hàm số _{\(y\ =\ \frac{x\ -2}{x\ +1}\)} và đường thẳng y = x - 2 cắt nhau tại hai điểm phân biệt có tung độ lần lượt là

y₁, y₂ . y₁ + y₂ bằng:

A. y₁ + y₂ = -4

B. y₁ + y₂ = 2

C. y₁ + y₂ = 4

D. y₁ + y₂ = -2

Câu 24. Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn cho số phức z = 2 + 2i ; M’ là điểm biểu diễn cho số phức

z'= _{\(\frac{3i}{2}Z\)} Tính diện tích tam giác OMM’.

A. S_{\(\triangle\)OMM '} = 4

B. S_{\(\triangle\)OMM '} = 6

C. S_{\(\triangle\)OMM '} = 3

D. S _{\(\triangle\)OMM '} = _{\(\frac{15}{2}\)}

Câu 25. Một khối chóp tam giác đều có cạnh đáy là a, cạnh bên bằng\(a\sqrt{3}\) . Tính thể tích khối chóp đó:

A. \(\frac{a^3\sqrt{2}}{6}\)

B. \(\frac{a^3\sqrt{6}}{3}\)

C. \(\frac{a^3\sqrt{3}}{6}\)

D. \(\frac{a^3\sqrt{6}}{4}\)

Câu 26. Tổng diện tích các mặt của một khối lập phương là 54cm² . Tính thể tích của khối lập phương đó.

A. 9 cm³

B. 27 cm³

C. 81 cm³

D. 18 cm³

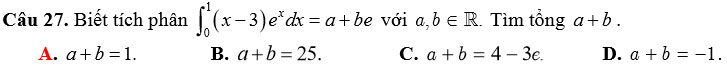
Câu 28. Cho số phức z có phần ảo bằng 164 và với số nguyên dương n thỏa mãn _{\(\frac{z}{z+n}=4i\) ^.} Tìm n?

A. n = 679.

B. n = -656.

C. n = 697.

D. n = 656.

Câu 29. Tìm c biết a,b và c là các số nguyên dương thỏa mãn c = (a + bi )³ -107i.

A. c =198.

B. c =189.

C. c = 198 hoặc c = -198.

D. c = -198.

Câu 30. Đường thẳng d đi qua H(3;-1;0) và vuông góc với (Oxz) có phương trình là:

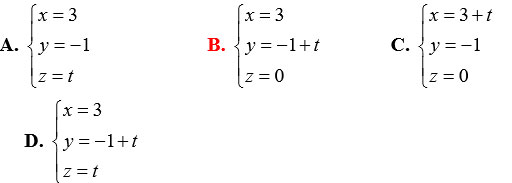
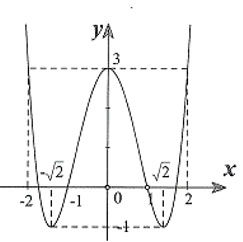
Câu 31. Hàm số y = f ( x) = ax⁴ + bx² + c (a\(\ne\)0) có đồ thị như hình vẽ. Hàm số y = f ( x) là hàm số nào trong bốn hàm số sau:

A. y = (x² + 2)² -1

B. y = -x⁴ + 2x² + 3

C. y = (x² - 2)² -1

D = -x⁴ + 4x² + 3

Câu 32. Cho hàm số y = -x³ + 3x² - x +1. Gọi x_1, x₂ có giá trị bằng là các điểm cực trị của hàm số trên. Khi đó \(x_2^1\ +\ x_2^2\) có giá trị bằng:

A. \(\frac{35}{9}\)

B. \(\frac{14}{3}\)

C. \(-\frac{35}{9}\)

D. \(\frac{10}{3}\)

Câu 33. Cho hàm số y = \(\frac{mx\ -\ 1}{2x+m}\) Giá trị của tham số m để tiệm cận đứng của đồ thị hàm số cho đi qua điểm A \(\left(-1;\ \sqrt{2}\right)\) là:

A. m = 2

B. m = -2

C. m = -1

D. m = \(\sqrt{2}\)

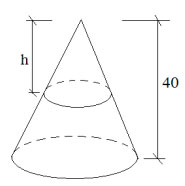
Câu 34. Một vật N1 có dạng hình nón có chiều cao bằng 40cm. Người ta cắt vật N₁ bằng một mặt cắt song song với mặt đáy của nó để được một hình nón nhỏ N₂ có thể tích bằng _{\(\frac{1}{8}\)} thể tích N₁.Tính chiều cao h của hình nón N₂?

A. 5 cm

B. 10 cm

C. 20 cm

D. 40 cm

Câu 35. Đường thẳng y = ax + b cắt đồ thị hàm số y = \(\frac{1\ -\ 2x}{1+\ 2x}\) tại hai điểm A và B có hoành độ lần lượt bằng -1 và 0. Lúc đó giá trị của a và b là:

A. a = 1 và 2 b = 1

B. a = 4 và b = 1

C. a = - 2 và b = 1

D. a = -3 và b = 2

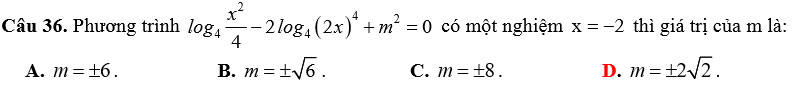
Hỏi khẳng định nào sau đây là khẳng định đúng?

A. Hàm số không có đạo hàm tại x = 0 nhưng vẫn đạt giá trị cực đại tại x = 0 .

B. Đồ thị hàm số có hai tiệm cận đứng x = -1, x = 1 và một tiệm cận ngang y = 3.

C. Hàm số đạt cực đại tại điểm x = -1.

D. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng y = -3, y = 3 .

Câu 42. các số phức z₁, z₂ , z₃, z₄ có các điểm biểu diễn trên mặt phẳng phức là A, B, C, D (như hình vẽ). Tính P = z₁ + z₂ + z₃ + z₄

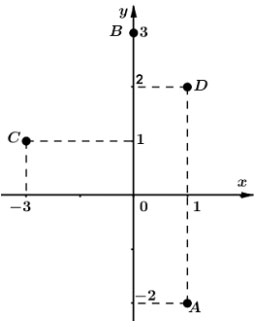
_{A. P = 2}

B. \(P\ =\ \sqrt{5}\)

C. P = 3

D. \(\frac{2}{3}\)

Câu 43. Cho hình chóp S.ABCD có đáy là hình chữ nhật. Mặt phẳng đi qua A, trọng tâm G của tam giác SBC và song song với BC cắt SB, SC lần lượt tại M, N. Tỷ số _{\(\frac{V_{SAMND}}{V_{SABCD}}\) là:}

_{A. \(\frac{1}{9}\)}

_{B. \(\frac{1}{4}\)}

_{C. \(\frac{5}{9}\)}

_{D. \(\frac{2}{3}\)}

Câu 44. Một hình nón được đặt bên trong hình lập phương (như hình vẽ). Hãy tính tỉ lệ nón và hình lập phương:

\(\frac{V_n}{V_{Lp}}\)

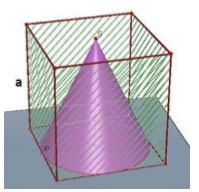
A. 0,541.

B. 0,413.

C. 0,262.

D. 0,654.

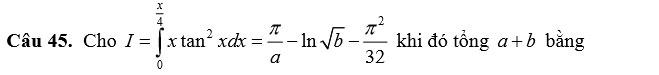
A. 4.

B. 8.

C. 10.

D. 6.

Câu 46. Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là _{\(f\ \left(t\right)\ =\ 4t^3\ -\ \frac{t^4}{2}\)} (người). Nếu xem f '(t ) là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ mấy?

A. 4.

B. 6.

C. 5.

D. 3.

Câu 47. Hàm số \(y\ =\ \sqrt{2x-x^2}\) đồng biến trên khoảng:

A. (0;1)

B. (1;2)

C. (- \(00\);1)

D. \(\left(1;\ +00\right)\)

Câu 48. Với các giá trị nào của m thì đồ thị (C) của hàm số y = x³ + 3x² - 2 cắt đường thẳng d : y = m tại 3 điểm phân biệt?

A. -2 < m < 0.

B. 0 < m < 2.

C. -2 < m < 2.

D. m < -2 ∨ m > 2.

Câu 49. Phương trı̀nh 2^x-1 - 2^{x2- x} = (x -1)² có bao nhiêu nghiêm?

A. 2.

B. 3.

C. 4.

D. 1.

Câu 50. Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là 1dm và 2dm sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Bán kính đáy của hình nón đã cho là:

A. \(\frac{8}{3}dm\)

B. \(\sqrt{2}dm\)

C. \(2\sqrt{2}dm\)

D. \(\frac{4}{3}dm\)

ĐÁP ÁN - TÓM TẮT CÁCH GIẢI