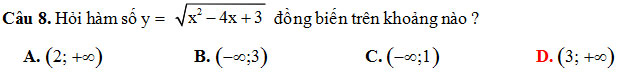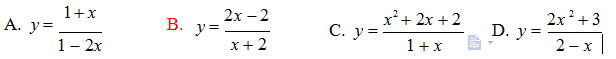Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Đề thi thử THPT Quốc gia môn Toán năm 2018, Sở GD&ĐT Nghệ An

Thi thử THPT quốc gia môn Toán

Đề thi thử THPT quốc gia môn Toán trường THPT Cửa Lò

VnDoc.com xin giới thiệu tới bạn đọc tài liệu: Đề thi thử THPT quốc gia môn Toán năm 2018, sở GD&ĐT Nghệ An, bộ tài liệu sẽ giúp các bạn học sinh rèn luyện cách giải các bài Toán một cách hiệu quả nhất. Mời các bạn học sinh và thầy cô tham khảo.

Đề thi thử THPT quốc gia môn Toán năm 2018, sở GD&ĐT Hưng Yên

Đề thi thử THPT Quốc Gia môn Toán năm 2018

Đề thi thử THPT quốc gia môn Toán năm 2018, sở GD&ĐT Nghệ An

Câu 1: Hỏi hàm số y = x⁴ - 2x² + 3 đồng biến trên các khoảng nào?

A. R

B. (-1; 0) và (0;1)

C. (-∞;-1) và (0;1)

D. (-1; 0) và (1; +∞)

Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có đúng một cực trị.

B. Hàm số có giá trị cực tiểu bằng 2.

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3.

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1.

Câu 4: Hàm số _{$y\ =\ \frac{x^{^2}\ -\ 4x\ +\ 1}{x+\ 1}$}có hai điểm cực trị là x₁, x₂ , khi đó tích x₁.x₂ bằng:

A. -5

B. 5

C. -2

D. 2

Câu 5: Tìm tất cả các giá trị của m để đồ thị hàm số y = x⁴ - 2mx² +1+ m có ba điểm cực trị là ba đỉnh của tam giác đều:

A. $m\ =\ \sqrt[3]{3}$ $m\ =\ \sqrt[3]{3}$

B. m ≥ 0

C. $m\ =\ \frac{3}{2}$ $m\ =\ \frac{3}{2}$

D. $m>\sqrt[3]{3}$ $m>\sqrt[3]{3}$

Câu 6: Tìm giá trị lớn nhất của hàm số $y\ =\ \frac{3x\ -\ 1}{x\ -3}$ $y\ =\ \frac{3x\ -\ 1}{x\ -3}$ trên đoạn [0;2]

A. $-\ \frac{1}{3}$ $-\ \frac{1}{3}$

B. - 5

C. 5

D. $\frac{1}{3}$ $\frac{1}{3}$

Câu 7: Cho các hàm số $f_{\left(x\right)}\ =\ \frac{10x^2\ -\ 6x-7}{\sqrt{2x\ -\ 3}},\ g\ \left(x\right)=\left(a\ x^2\ +\ bx+\ c\right)\ \sqrt{2x-3,\ }\ x>\ \frac{3}{2}$ $f_{\left(x\right)}\ =\ \frac{10x^2\ -\ 6x-7}{\sqrt{2x\ -\ 3}},\ g\ \left(x\right)=\left(a\ x^2\ +\ bx+\ c\right)\ \sqrt{2x-3,\ }\ x>\ \frac{3}{2}$. Để hàm số g (x) là một nguyên hàm của hàm sốf (x) thì giá trị của a, b, c là:

A. a = b = 2, c =-1.

C. a = b = 2, c =1.

B. a = 2, b =-2, c =-1.

D. a = 2, b =-2, c =1.

Câu 9: Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số nào sao đây?

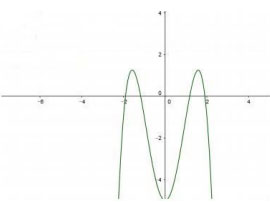
Câu 10: Cho hàm số y = ax⁴ + bx² + c có đồ thi ̣như hı̀nh vẽ bên. Mênh đề nào dưới đây đúng?

A. a > 0, b < 0, c > 0

B. a < 0, b > 0, c < 0

C. a < 0, b < 0, c < 0

D. a > 0, b < 0, c < 0

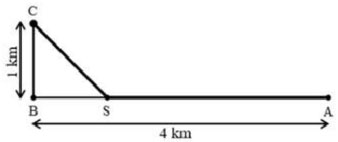
Đề thi thử THPT quốc gia môn Toán năm 2018

Câu 11: Một đường dây điện được nối từ nhà máy điện trên đất liền ở vị trí A đến vị trí C trên một hòn đảo. Khoảng cách ngắn nhất từ C đến đất liền là BC= 1km, khoảng cách từ A đến B là 4km. Người ta chọn một vị trí là điểm S nằm giữa A và B để mắc đường dây điện đi từ A đến S, rồi từ S đến C như hình vẽ dưới đây. Chi phí mỗi km dây điện trên đất liền mất 3000USD, mỗi km dây điện đặt ngầm dưới biển mất 5000USD. Hỏi điểm S phải cách A bao nhiêu km để chi phí mắc đường dây điện là ít nhất.

Đề thi thử THPT quốc gia môn Toán năm 2018

A. 3km

B. 1km

C. 2km

D. 1, 5km

Đề thi thử THPT quốc gia môn Toán năm 2018

Câu 21. Anh An vay ngân hàng 300 triệu đồng theo phương thứ trả góp để mua nhà. Nếu cuối tháng bắt đầu từ tháng thứ nhất anh An trả 5,5 triệu đồng (trừ tháng cuối) và chịu tiền chưa trả là 0,5% mỗi tháng (biết lãi suất không đổi) thì sau bao nhiêu lâu An trả hết số tiền trên? Biết rằng số tiền tháng cuối anh An trả phài nhỏ hơn 5,5 triệu đồng.

A. 64 tháng

B. 63 tháng

C. 54 tháng

D. 55 tháng

Đề thi thử THPT quốc gia môn Toán năm 2018

A. 5

B. 9

C. -5

D.1

Câu 27: Một ca nô đang chạy trên Hồ Tây với vận tốc 20m/s thı̀ hết xăng. Từ thời điểm đó, ca nô chuyển động chậ đến lúc ca nô dừng hẳn đi được bao nhiêu mét?

A. 10m

B. 20m

C. 30m

D. 40m

Câu 28: Cho hình phẳng giới hạn bởi đường cong $y=\ 2\sqrt{1-x^2},\ y\ =\left(1-\ x\right)$ $y=\ 2\sqrt{1-x^2},\ y\ =\left(1-\ x\right)$. Thể tích của khối tròn xoay thu được khi quay hình này quanh trục trục Ox:

A. $\frac{\pi}{6}$ $\frac{\pi}{6}$

B. $\frac{\pi}{3}$ $\frac{\pi}{3}$

C. $\frac{4\pi}{3}$ $\frac{4\pi}{3}$

D. $\frac{5\pi}{6}$ $\frac{5\pi}{6}$

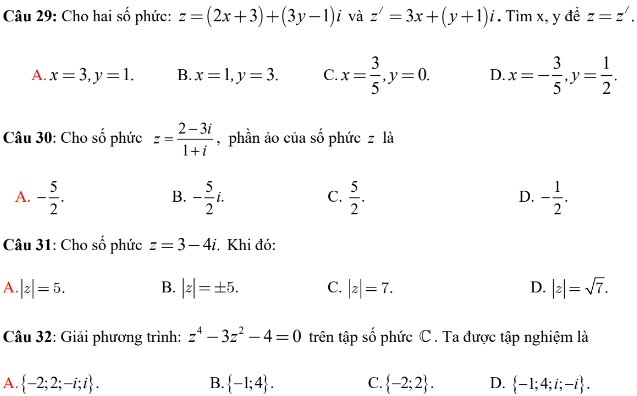
Câu 33: Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện ΙZ + 3 -4Ι ≤ 9 là:

A. Hình tròn giới hạn bởi đường tròn tâm I (-3; 4), bán kính R = 9, không kể đường tròn đó.

B. Hình tròn giới hạn bởi đường tròn tâm I (-3; 4), bán kính R = 9, kể cả đường tròn đó.

C. Đường tròn tâm I (-3; 4), bán kính R = 9.

D. Hình tròn giới hạn bởi đường tròn tâm I (3; -4), bán kính R = 9, kể cả đường tròn đó.

Đề thi thử THPT quốc gia môn Toán năm 2018

Câu 36: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, AB = a, ÐBAC = 30⁰, SB^(ABC) và SB = 2a. Tìm thể tích của khối chóp S.ABC.

A. $\frac{a^3}{6}$ $\frac{a^3}{6}$

B. $\frac{a^3}{2}$ $\frac{a^3}{2}$

C.$a^3$

D. $\frac{a^3}{3}$ $\frac{a^3}{3}$

Câu 37: Cho hình lăng trụ tam giác đều ABC.A' B' C' có độ dài cạnh bên bằng độ dài cạnh đáy và bằng. Tìm thể tích khối trụ có hai đường tròn đáy lần lượt nội tiếp DABC, DA'B'C'.

A. $V\ =\ \frac{\pi a^3}{12}$ $V\ =\ \frac{\pi a^3}{12}$

B. $V\ =\ \frac{\pi a^3}{36}$ $V\ =\ \frac{\pi a^3}{36}$

C. $V\ =\ \frac{a^3}{12}$ $V\ =\ \frac{a^3}{12}$

D. $V\ =\ \frac{\pi a^3}{3}$ $V\ =\ \frac{\pi a^3}{3}$

Câu 38: Cho tam giác ABC vuông tại A, AC = a, _{$AB\ \ =\ \sqrt{3}$}Tìm diện tích toàn phần của hình nón được tạo ra khi cho đường gấp khúc ACB quay quanh cạnh AB cố định.

A. $S_{tp}=\ 5a^2\pi$ $S_{tp}=\ 5a^2\pi$

B. $S_{tp}\ =\ 3a^2\ \pi\ \$ $S_{tp}\ =\ 3a^2\ \pi\ \ $

C. $S_{tp}\ \ =\ 2a^2\pi$ $S_{tp}\ \ =\ 2a^2\pi$

D. $S_{tp\ }=\ 3a^2$ $S_{tp\ }=\ 3a^2$

Câu 39: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi E là điểm thuộc cạnh SB sao cho BE = 2SE. Tính tỉ số: _{$\frac{V_{B.EMN}}{V_{S.ABCD}}$}

A. $\frac{1}{12}$ $\frac{1}{12}$

B. $\frac{1}{6}$ $\frac{1}{6}$

C. $\frac{1}{16}$ $\frac{1}{16}$

D. $\frac{3}{16}$ $\frac{3}{16}$

Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA $\perp$ $\perp$(ABCD), SA = 2a. Góc giữa SC và đáy có số đo là 45⁰. Tìm diện tích mặt cầu ngoại tiếp hình chóp S.ABCD.

A. $32\pi a^2$ $32\pi a^2$

B. $6\pi a^2$ $6\pi a^2$

C. $8\pi a^2$ $8\pi a^2$

D. $24\pi a^2$ $24\pi a^2$

Câu 41: Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng _{$\frac{1}{3}$}chiều cao của phễu. Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên thì chiều cao của nước bằng bao nhiêu? Biết rằng chiều cao của phễu là 15cm.

A. 0,188(cm).

B. 0,216(cm).

C. 0,3(cm).

D. 0,5 (cm).

Đề thi thử THPT quốc gia môn Toán năm 2018

Câu 42: Một hình trụ có trục OO' = 2a, ABCD là hình vuông có cạnh bằng 2a có đỉnh nằm trên hai đường tròn đáy sao cho tâm của hình vuông trùng với trung điểm của OO'. Thể tích của hình trụ bằng bao nhiêu?

A. $10a^{3\pi}$ $10a^{3\pi}$

B. $5a^{3\pi}$ $5a^{3\pi}$

C. $\frac{10}{3}a^3\pi$ $\frac{10}{3}a^3\pi$

D. $15a^3\pi$ $15a^3\pi$

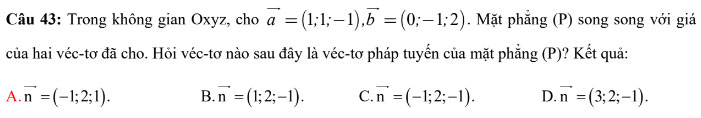
Câu 44: Trong không gian Oxyz, cho ba A(2;0;0),B(0;-3;0), C(0;0;4). Tìm phương trình mặt phẳng (P) qua ba điểm A, B, C. Kết quả

A. 6x - 4 y + 3z -1 = 0.

B. 6x - 4 y + 3z -12 = 0.

C. _{$\frac{x}{2}\ -\frac{y}{3}\ +\ \frac{z}{4}\ =\ 0$}
D. 6x - 4 y - 3z -12 = 0.

Câu 45: Trong không gian Oxyz, cho hai điểm A(-4;3;1),B(2;1;-1). Tìm phương trình mặt phẳng trung trực của đoạn thẳng AB. Kết quả:

A. 3x - y - z + 5 = 0.

B. 3x - y - z +16 = 0.

C. 3x - y - z - 6 = 0.

D. x - 2 y - 5 = 0.

Câu 46: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 2;3), B (0; -1; 2). Phương trình nào sau đây là phương trình tham số của đường thẳng AB?

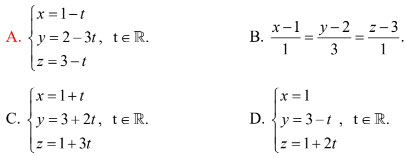
Câu 47: Trong không gian Oxyz, cho 2 điểm A(-5;1;-6),B(0;2;1). Tìm toạ độ các điểm M trên trục Oy sao cho tam giác MAB vuông tại M. Kết quả:

A. M (0;1;0) hay M (0;-4;0).

B. M (0;-1;0) hay M (0;4;0).

C. M (0;-1;0) hay M (0;-4;0).

D. M (0;1;0) hay M (0;4;0).

Câu 48: Trong không gian Oxyz, cho điểm M (1;-1;-1) và hai mặt phẳng (a) : x - 2 y +3z -5 = 0, (b) : 2x - y - z +1= 0.Tìm phương trình của mặt phẳng (P) qua M, đồng thời vuông góc với cả hai mặt phẳng đã cho. Kết quả:

A. 5x + 7 y + 3z + 5 = 0.

B. 5x - 7 y + 3z - 9 = 0.

C. 5x - 7 y - 3z -15 = 0.

D. 5x + 7 y - 3z -1 = 0.

Câu 49: Tìm phương trình đường thẳng đi qua điểm A(2;-5;6), cắt Ox và song song với mặt phẳng x + 5y - 6z = 0. Kết quả:

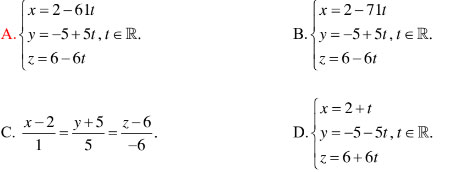
Câu 50. Cho ba tia Ox, Oy, Oz đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt OC = 1; các điểm A, B thay đổi trên Ox, Oy sao cho OA + OB = OC. Tìm giá trị bé nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC.

A. $\frac{\sqrt{6}}{4}$ $\frac{\sqrt{6}}{4}$

B. $\frac{\sqrt{6}}{3}$ $\frac{\sqrt{6}}{3}$

C. $\sqrt{6}$ $\sqrt{6}$

D. $\frac{\sqrt{6}}{2}$ $\frac{\sqrt{6}}{2}$

Chia sẻ, đánh giá bài viết

2.042