Đề thi thử THPT Quốc gia môn Toán trường THPT Nguyễn Trường Tộ, Bình Định năm 2015

Đề thi thử THPT Quốc gia môn Toán có đáp án

Đề thi thử THPT Quốc gia môn Toán trường THPT Nguyễn Trường Tộ, Bình Định năm 2015 gồm 10 câu hỏi có đáp án đi kèm, là tài liệu ôn tập môn Toán hữu ích dành cho các bạn học sinh, giúp các bạn củng cố và rèn luyện kiến thức, sẵn sàng cho kì thi THPT Quốc gia 2016 sắp tới. Mời các bạn tham khảo.

Bộ 10 đề thi thử THPT Quốc gia môn Toán năm 2016

260 bài toán phương trình và hệ phương trình trong ôn thi đại học

Tuyển tập Bộ 3 câu phân loại trong các đề thi thử THPT Quốc gia 2015 môn Toán

SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH ĐỊNH

TRƯỜNG THPT NGUYỄN TRƯỜNG TỘ

ĐỀ THI THỬ KÌ THI THPT QUỐC GIA NĂM 2015

Môn TOÁN

Thời gian làm bài 180 phút

------------***------------

Câu 1 (2,0 điểm). Cho hàm số: y = x⁴ - 2(m² + 1)x² + 1 (1)

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) khi m = 0.

b) Tìm các giá trị của tham số m để hàm số (1) có 3 điểm cực trị thỏa mãn giá trị cực tiểu đạt giá trị lớn nhất.

Câu 2 (1,0 điểm).

a) Giải phương trình: sin2x - cosx + sinx = 1 (x ∈ R)

b) Giải bất phương trình:

Câu 3 (1,0 điểm). Tính tích phân:

Câu 4 (0,5 điểm). Cho số phức z thỏa mãn điều kiện:

Câu 5 (1,0 điểm). Cho hình lăng trụ ABC.A'B'C', ΔABC đều có cạnh bằng a, AA' = a và đỉnh A' cách đều A, B, C. Gọi M, N lần lượt là trung điểm của cạnh BC và A'B. Tính theo a thể tích khối lăng trụ ABC.A'B'C' và khoảng cách từ C đến mặt phẳng (AMN).

Câu 6 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz , cho mặt cầu có phương trình x² + y² + z² - 4x + 6y - 2z - 2 = 0. Lập phương trình mặt phẳng (P) chứa trục Oy và cắt mặt cầu (S) theo một đường tròn có bán kính r = 2√3.

Câu 7 (0,5 điểm). Giải bóng chuyền VTV Cup gồm 12 đội bóng tham dự, trong đó có 9 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C mỗi bảng 4 đội. Tính xác suất để 3 đội bóng của Việt Nam ở ba bảng khác nhau.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với đường cao AH có phương trình 3x + 4y + 10 = 0 và đường phân giác trong BE có phương trình x - y + 1 = 0. Điểm M(0;2) thuộc đường thẳng AB và cách đỉnh C một khoảng bằng √2. Tính diện tích tam giác ABC.

Câu 9 (1,0 điểm). Giải bất phương trình:

Câu 10 (1,0 điểm). Cho các số thực x; y thay đổi. Tìm giá trị nhỏ nhất của biểu thức:

Đáp án đề thi thử THPT Quốc gia môn Toán

Câu 1:

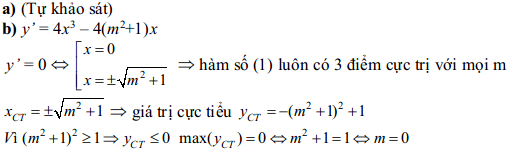
Câu 2:

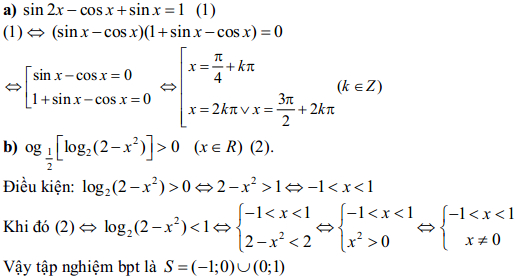
Câu 3:

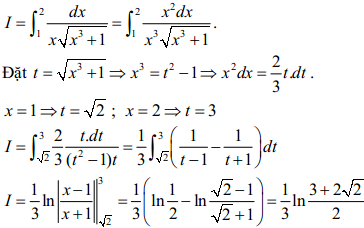
Câu 4:

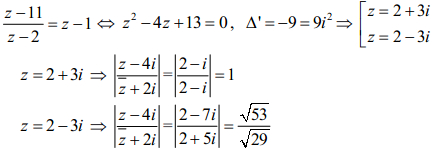
(Còn tiếp)