Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Gia Lộc, Hải Dương (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Gia Lộc, Hải Dương (Lần 1) là đề thi thử đại học môn Toán có đáp án đi kèm dành cho các bạn thi sinh luyện đề, ôn tập và củng cố kiến thức, nhằm chuẩn bị sẵn sàng cho kỳ thi THPT Quốc gia 2016 sắp diễn ra.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Đoàn Thượng, Hải Dương (Lần 1)

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Đại học Vinh (Lần 2)

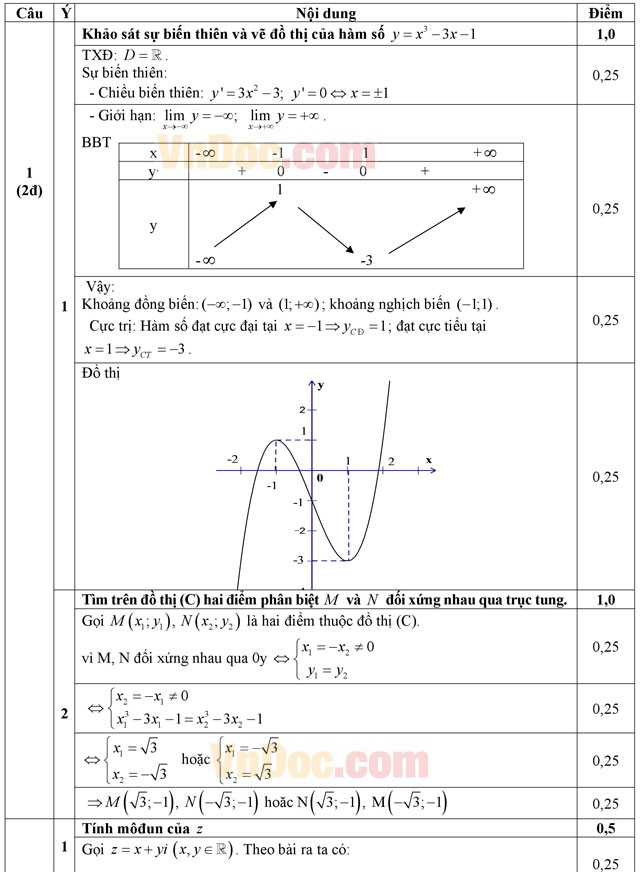
Câu 1 (2,0 điểm)

Cho hàm số: y = x³ - 3x - 1 (C).

1. Khảo sát sự thiên và vẽ đồ thị của hàm số y = x³ - 3x - 1 (C).
2. Tìm trên đồ thị (C) hai điểm phân biệt M và N đối xứng với nhau qua trục tung.

Câu 2 (1,0 điểm)

1. Cho số phức z thỏa mãn: . Tính môđun của z.
2. Giải bất phương trình: log₄x² + log₂(2x - 1) + log_1/2(4x + 3) < 0.

Câu 3 (1,0 điểm)

1. Giải phương trình: 2cos5x.cos3x + sinx = cos8x.
2. Một hộp có 9 thẻ giống nhau được đánh số liên tiếp từ 1 đến 9. Rút ngẫu nhiên đồng thời hai thẻ (không kể thứ tự) rồi nhân hai số ghi trên hai thẻ với nhau. Tính xác suất để kết quả nhận được là một số chẵn.

Câu 4 (1,0 điểm)

Tính tích phân: .

Câu 5 (1,0 điểm)

Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a (a > 0), góc ABC = 60^o. Cạnh bên SA vuông góc với mặt đáy (ABCD), góc tạo bởi SC và mặt phẳng (ABCD) bằng 60^o. Gọi M là trung điểm của SB. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AM, SD theo a.

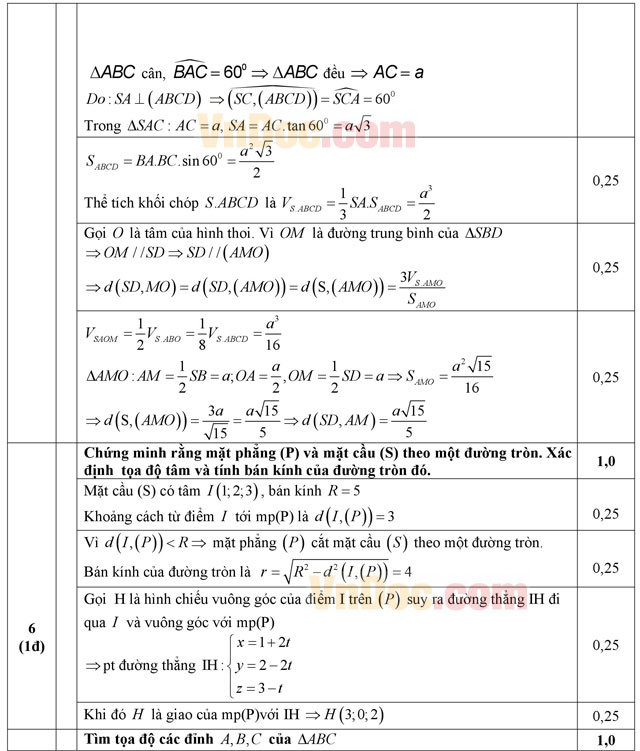
Câu 6 (1,0 điểm)

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x - 2y - z - 4 = 0 và mặt cầu (S): x2 + y2 + z2 - 2x - 4y - 6z - 11 = 0. Chứng minh rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn. Xác định tọa độ tâm và tính bán kính của đường tròn đó.

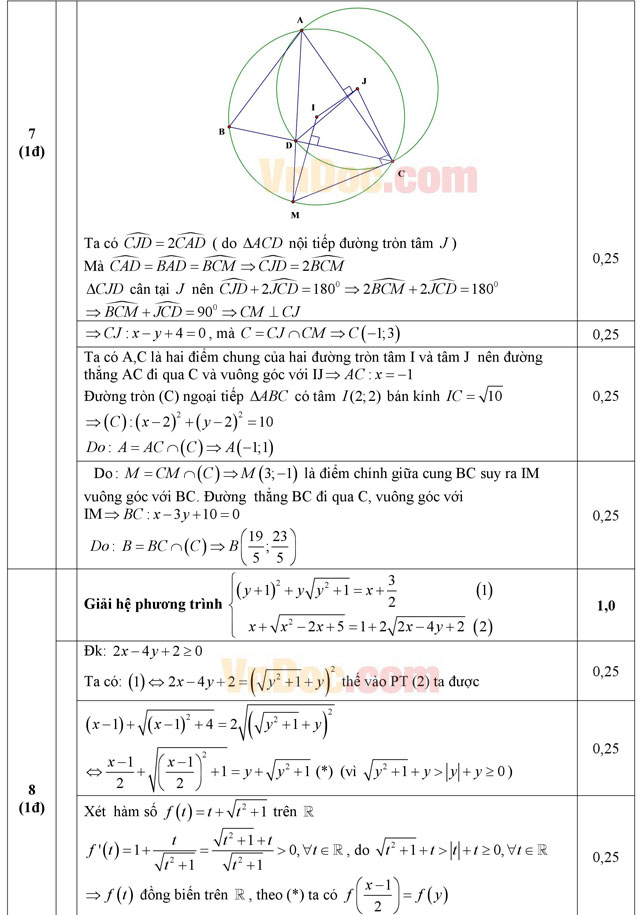
Câu 7 (1,0 điểm)
Trong mặt phẳng với hệ tọa độ Oxy, cho ΔABC nội tiếp đường tròn tâm I(2; 2), điểm D là chân đường phân giác trong của góc BAC. Đường thẳng AD cắt đường tròn ngoại tiếp ΔABC tại điểm thứ hai là M (khác A). Tìm tọa độ các điểm biết điểm J(-2; 2) là tâm đường tròn ngoại tiếp ΔACD và phương trình đường thẳng CM là: x + y - 2 = 0.

Câu 8 (1,0 điểm)

Giải hệ phương trình: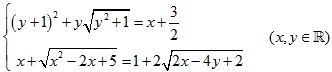

Câu 9 (1,0 điểm)

Cho các số thực dương a, b, c thỏa mãn: 4(a³ + b³) + c³ = 2(a + b + c)(ac + bc - 2).

Tìm giá trị lớn nhất của biểu thức:

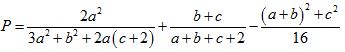
Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán