Hệ thức lượng trong tam giác

GiaiToan xin giới thiệu tời bạn đọc tài liệu Hệ thức lượng trong tam giác bao gồm công thức hệ thức lượng trong tam giác vuông, hệ thức lượng trong tam giác thường và hướng dẫn giải tam giác. Đây là tài liệu học tập hữu ích dành cho các bạn tham khảo, luyện tập nhằm củng cố kiến thức về các hệ thức lượng trong tam giác Toán 10. Mời các bạn học sinh tham khảo, chuẩn bị tốt cho kì thi sắp tới. Chúc các bạn học tập tốt!

Công thức hệ thức lượng trong tam giác

1. Hệ thức lượng trong tam giác vuông

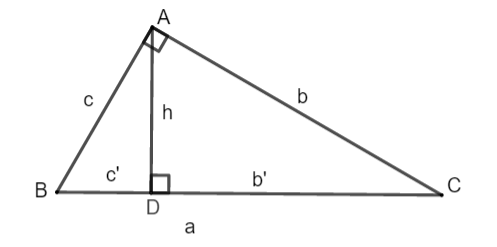
Cho tam giác ABC vuông tại A, đường cao AD ta có:

a. Định lý Pi – ta – go

- Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông \({{a}^{2}}={{b}^{2}}+{{c}^{2}}\)

b. Hệ thức về cạnh và đường cao trong tam giác vuông.

\(\begin{align} & {{c}^{2}}=c'.a; \\ & {{b}^{2}}=b'.a; \\ & {{h}^{2}}=c'.b'; \\ & c.b=h.a; \\ & \frac{1}{{{h}^{2}}}=\frac{1}{{{c}^{2}}}+\frac{1}{{{b}^{2}}} \\ \end{align}\)

2. Hệ thức lượng trong tam giác thường

a. Định lí cosin

- Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai góc còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.

Ta có hệ thức sau:

\(a^2=b^2+c^2-2.b.c.cos\hat{A}\)

\(b^2=a^2+c^2-2.a.c.cos\hat{B}\)

\(c^2=a^2+b^2-2a.b.cos\hat{C}\)

b. Tính độ dài đường trung tuyến của tam giác

- Cho tam giác ABC có cạnh AB = c, AC = b, BC = a. Gọi độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B, C của tam giác ABC là: _{\(m_a,m_b,m_c\)} ta có:

\(m_a^2=\frac{b^2+c^2}{2}+\frac{a^2}{4}\)

\(m^2_b=\dfrac{a^2+c^2}{2}+\dfrac{b^2}{4}\)

\(m^2_c=\dfrac{b^2+a^2}{2}+\dfrac{c^2}{4}\)

c. Định lí sin

- Trong tam giác ABC bất kì, tỉ số giữa cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là:

\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\)

Với R là bán kính đường tròn ngoại tiếp tam giác

d. Công thức diện tích tam giác

- Giả sử \(h_a,h_b,h_c\) là các đường cao lần lượt kẻ từ đỉnh A, B, C của tam giác ABC.

Diện tích tam giác ABC được tính theo một trong các công thức sau:

\(\begin{align} & S=\frac{1}{2}.{{h}_{a}}.BC=\frac{1}{2}{{h}_{b}}.AC=\frac{1}{2}{{h}_{c}}.AB \\ & S=\frac{1}{2}a.b.\sin \widehat{C}=\frac{1}{2}a.c.\sin \widehat{B}=\frac{1}{2}c.b.\sin \widehat{A} \\ & S=\frac{a.b.c}{4.R} \\ & S=p.r \\ & S=\sqrt{p.\left( p-a \right)\left( p-b \right)\left( p-c \right)} \\ \end{align}\)

Với p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC.

3. Bài tập Hệ thức lượng trong tam giác

Bài tập 1: Cho tam giác ABC có AB = 4, AC = 5, \(\cos \widehat{A}=\frac{3}{5}\). Tính cạnh BC và độ dài đường cao kẻ từ A.

Hướng dẫn giải

Áp dụng định lí cosin ta có:

\(\begin{align} & B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}-2AB.AC.\cos \widehat{A} \\ & \Rightarrow B{{C}^{2}}={{4}^{2}}+{{5}^{2}}-2.4.5.\frac{3}{5}=29 \\ & \Rightarrow BC=\sqrt{29} \\ \end{align}\)

Vì \({{\sin }^{2}}A+{{\cos }^{2}}A=1\Rightarrow \sin A=\sqrt{1-{{\cos }^{2}}A}=\sqrt{1-{{\left( \frac{3}{5} \right)}^{2}}}=\frac{4}{5}\)

Theo công thức diện tích tam giác ta có:

\({{S}_{ABC}}=\frac{1}{2}.AB.AC.\sin \widehat{A}=\frac{1}{2}.4.5.\frac{4}{5}=8\)

Mặt khác ta có: \({{S}_{ABC}}=\frac{1}{2}.a.{{h}_{a}}=\frac{1}{2}.\sqrt{29}.{{h}_{a}}\)

\(\Leftrightarrow \frac{1}{2}.\sqrt{29}.{{h}_{a}}=8\Rightarrow {{h}_{a}}=\frac{16}{\sqrt{29}}\)

Vậy độ dài đường cao kẻ từ A là \({{h}_{a}}=\frac{16}{\sqrt{29}}\)

Bài tập 2: Cho tam giác ABC có AB = 3, AC = 7, BC = 8.

a. Tính diện tích tam giác ABC.

b. Tính bán kính đường tròn nội tiếp, ngoại tiếp tam giác.

c. Tính độ dài đường cao kẻ từ đỉnh A.

Hướng dẫn giải

a. Nửa chu vi tam giác ABC là: \(p=\frac{AB+AC+BC}{2}=\frac{3+7+8}{2}=9\)

Áp dụng công thức He – rong ta có:

\({{S}_{ABC}}=\sqrt{p\left( p-AB \right)\left( p-AC \right)\left( p-BC \right)}=6\sqrt{3}\)

b. Ta có: \({{S}_{ABC}}=\frac{AB.AC.BC}{4R}\Rightarrow R=\frac{AB.AC.BC}{4{{S}_{ABC}}}=\frac{3.7.8}{4.6\sqrt{3}}=\frac{7\sqrt{3}}{3}\)

Vậy bán kính đường tròn ngoại tiếp tam giác ABC là \(R=\frac{7\sqrt{3}}{3}\)

Ta lại có: \({{S}_{ABC}}=p.r\Rightarrow r=\frac{{{S}_{ABC}}}{p}=\frac{6\sqrt{3}}{9}=\frac{2\sqrt{3}}{3}\)

Vậy bán kính đường tròn nội tiếp tam giác ABC là \(r=\frac{2\sqrt{3}}{3}\)

c. Gọi độ dài đường cao kẻ từ H là h

Ta có: \({{S}_{ABC}}=\frac{1}{2}.h.BC\Rightarrow h=\frac{2.{{S}_{ABC}}}{BC}=\frac{2.6\sqrt{3}}{8}=\frac{3\sqrt{3}}{2}\)

Bài tập 3: Cho tam giác ABC vuông tại A, đường cao AH, AB = 6, AC = 3.

a. Tính độ dài BC và đường cao AH của tam giác ABC

b. Tính S, R

Hướng dẫn giải

Ta có: \(B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}\Rightarrow BC=3\sqrt{5}\)

\(\frac{1}{A{{H}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{A{{C}^{2}}}\Rightarrow AH=\frac{6\sqrt{5}}{5}\)

\(\begin{align} & {{S}_{ABC}}=\frac{1}{2}.AB.AC=\frac{1}{2}.6.3=9 \\ & {{S}_{ABC}}=\frac{AB.AC.BC}{4R}\Rightarrow R=\frac{AB.AC.BC}{4{{S}_{ABC}}}=\frac{6.3.3\sqrt{5}}{4.9}=\frac{3\sqrt{5}}{2} \\ \end{align}\)

Bài tập 4: Cho tam giác ABC biết \(BC=2\sqrt{3},AC=2\sqrt{2},AB=\sqrt{6}-\sqrt{2}\). Tính góc lớn nhất của tam giác.

Hướng dẫn giải

Theo đề bài ta có: \(AB< AC< BC \Rightarrow \widehat{C}<\widehat{B}<\widehat{A}\)

Vậy \(\widehat{A}\) là góc lớn nhất

Theo định lí cosin ta có:

\(\begin{align} & \cos \widehat{A}=\frac{A{{C}^{2}}+A{{B}^{2}}-B{{C}^{2}}}{2AC.AB}=\frac{{{\left( 2\sqrt{2} \right)}^{2}}+{{\left( \sqrt{6}-\sqrt{2} \right)}^{2}}-{{\left( 2\sqrt{3} \right)}^{2}}}{2.2\sqrt{2}.\left( \sqrt{6}-\sqrt{2} \right)}=\frac{4-4\sqrt{3}}{8\sqrt{3}-8}=\frac{1}{2} \\ & \Rightarrow \widehat{A}={{120}^{0}} \\ \end{align}\)

Vậy góc lớn nhất là góc A có số đo là \({{120}^{0}}\)

Bài tập 5: Cho tam giác ABC, chứng minh rằng:

1. \(\cos \frac{\widehat{A}}{2}=\sqrt{\frac{p\left( p-a \right)}{bc}}\)

2. \(\sin \widehat{A}+\sin \widehat{B}+\sin \widehat{C}=4\cos \frac{\widehat{A}}{2}.\cos \frac{\widehat{B}}{2}.\cos \frac{\widehat{C}}{2}\)

Hướng dẫn giải

Trên tia đối của tia AC lấy điểm D thỏa mãn AD = AB = c suy ra tam giác ABD cân tại A và \(\widehat{ADB}=\frac{1}{2}\widehat{A}\)

Áp dụng định lí cosin cho tam giác ABD có:

\(\begin{align} & B{{D}^{2}}=A{{B}^{2}}+A{{D}^{2}}-2AB.AD.\cos \widehat{BAD} \\ & \Rightarrow B{{D}^{2}}=2{{c}^{2}}-2{{c}^{2}}.\cos \left( {{180}^{0}}-\widehat{A} \right) \\ & =2{{c}^{2}}\left( 1+\cos \widehat{A} \right)=2{{c}^{2}}\left( 1+\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc} \right) \\ & =\frac{c}{b}\left( a+b+c \right)\left( b+c-a \right)=\frac{4c}{b}.p\left( p-a \right) \\ & \Rightarrow BD=2\sqrt{\frac{cp\left( p-a \right)}{b}} \\ \end{align}\)

Gọi M là trung điểm của BD suy ra \(AM\bot DB\)

Trong tam giác ADM vuông tại M ta có:

\(\begin{align} & \cos \frac{\widehat{A}}{2}=\cos \widehat{ADM}=\frac{DM}{DA}=\frac{BD}{2c}=\sqrt{\frac{p\left( p-a \right)}{bc}} \\ & \Rightarrow \cos \frac{\widehat{A}}{2}=\sqrt{\frac{p\left( p-a \right)}{bc}} \\ \end{align}\)

b. Áp dụng định lí cosin ta có:

\(\sin \widehat{A}+\sin \widehat{B}+\sin \widehat{C}=\frac{a}{2R}+\frac{b}{2R}+\frac{c}{2R}=\frac{p}{R}\)

Mặt khác \(\cos \frac{\widehat{A}}{2}=\sqrt{\frac{p\left( p-a \right)}{bc}}\) (chứng minh câu a) nên ta cũng suy ra được \(\cos \frac{\widehat{B}}{2}=\sqrt{\frac{p\left( p-b \right)}{ac}}, \cos \frac{\widehat{C}}{2}=\sqrt{\frac{p\left( p-c \right)}{ab}}\)

Kết hợp với công thức Herong: \(S=\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}=\frac{abc}{4R}\)

\(\begin{align} & \Rightarrow 4\cos \frac{\widehat{A}}{2}.\cos \frac{\widehat{B}}{2}.\cos \frac{\widehat{C}}{2}=4.\sqrt{\frac{p\left( p-a \right)}{bc}}.\sqrt{\frac{p\left( p-b \right)}{ac}}.\sqrt{\frac{p\left( p-c \right)}{ab}} \\ & =\frac{4p}{abc}.\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}=\frac{4pS}{abc}=\frac{p}{R} \\ \end{align}\)

\(\Rightarrow \sin \widehat{A}+\sin \widehat{B}+\sin \widehat{C}=4\cos \frac{\widehat{A}}{2}.\cos \frac{\widehat{B}}{2}.\cos \frac{\widehat{C}}{2}\)

4. Bài tập tự rèn luyện

Bài tập 1: Cho tam giác ABC có b = 14cm, c = 10cm, \(\widehat{A}={{145}^{0}}\). Tính a, \(\widehat{B};\widehat{C}\)

Bài tập 2: Cho tam giác ABC. Tính độ lớn các góc, độ dài đường trung tuyến xuất phát từ các đỉnh, bán kính đường tròn nội tiếp, ngoại tiếp trong các trường hợp sau:

a. b = 8, c = 5, \(\widehat{A}={{60}^{0}}\)

b. a = 10, b = 17, c = 21

Bài tập 3: Cho tam giác ABC có: AB = 10, AC = 2, \(\widehat{A}={{120}^{0}}\)

a. Tính BC và \(\cos \widehat{C}\)

b. Trên AC kéo dài lấy điểm D sao cho BD = 20. Tính AD.

Bài tập 4: Chứng minh các biểu thức sau:

1. \(a=b.\cos C+c.\cos B\)

2. \(\sin A=\sin B.\cos C+\sin C.\cos B\)

3. \(h.a=2.R.\sin B.\sin C\)

4. \(S=2.{{R}^{2}}.\sin A.\sin B.\sin C\)

5. \(S=R.r.\left( \sin A+\sin B+\sin C \right)\)

6. \(h.a=2R.\sin B.\sin C\)