Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Phân loại: Tài liệu Tính phí

Kẹo Ngọt Toán học lớp 9

Hoạt động 2 trang 44 SGK Toán 9 Chân trời sáng tạo

Hoạt động 2 trang 44 Toán 9: Ông An có một bể kính hình lập phương như Hình 2.

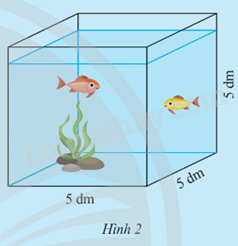
Ông An muốn làm thêm một bể kính mới hình lập phương có thể tích gấp n lần thể tích của bể kính cũ (bỏ qua bề dày của kính).

a) Gọi a (dm) là độ dài cạnh của bể kính mới. Thay mỗi ? bằng biểu thức thích hợp để nhận được các đẳng thức:

a³ = ? hay a = ?.

b) Tính giá trị của a khi n = 8 và khi n = 4 (kết quả làm tròn đến chữ số thập phân thứ hai).

1 3

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Xóa Đăng nhập để viết

3 Câu trả lời

Bi
a) a³ = (5.5.5).n = 125n hay a = $\sqrt[3]{{125n}} = 5\sqrt[3]{n}.$

b) Khi n = 8, ta được: $a = 5\sqrt[3]{n} = 5\sqrt[3]{8} = 5.2 = 10$

Khi n = 4, ta được: $a = 5\sqrt[3]{n} = 5\sqrt[3]{4} \approx 7,94.$

0 Trả lời 08/10/24
Bọ Cạp
a) Thể tích của bể kính cũ là: 5³ = 125 dm³

Gọi a (dm) là độ dài cạnh của bể kính mới

Khi đó, thể tích của bể kính mới là: a³

Do bể kính mới có thể tích gấp n lần thể tích của bể kính cũ nên ta có:

a³ = 125n hay $a=\sqrt[3]{125n}$

b) Với n = 8, ta có: $a=\sqrt[3]{125.8}= \sqrt[3]{1000}= \sqrt[3]{10^3}= 10$ dm

Với n = 4, ta có: $a=\sqrt[3]{125.4}= \sqrt[3]{500} \approx 7,94$ dm

0 Trả lời 08/10/24
Bánh Tét
Xem đáp án tại đây: Giải Toán 9 Chân trời sáng tạo Bài 2: Căn bậc ba

0 Trả lời 08/10/24