Đề thi chính thức THPT Quốc gia môn Toán năm 2015
Đề thi THPT Quốc gia môn Toán
Đề thi chính thức THPT Quốc gia môn Toán năm 2015 dưới đây là tài liệu ôn thi THPT Quốc Gia năm 2016 môn Toán cực hữu ích cho các em học sinh lớp 12. Mời các em tải Đề thi THPT Quốc gia môn Toán này về và chuẩn bị cho kỳ thi tốt nghiệp THPT Quốc Gia năm 2016 sắp diễn ra.
Đáp án đề thi THPT Quốc gia năm 2015 môn Toán
Đề thi minh họa và đáp án kỳ thi THPT Quốc gia năm 2016 môn Toán
| BỘ GIÁO DỤC VÀ ĐÀO TẠO | KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA 2015 |
| ĐỀ THI CHÍNH THỨC (Đề thi gồm 01 trang) |
Môn thi: Toán Thời gian làm bài: 180 phút; không kể thời gian phát đề |
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x³ - 3x.
Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x + 4/x trên đoạn [1;3].
Câu 3 (1,0 điểm).
a) Cho số phức z thỏa mãn (1 - i)z -1 + 5i = 0. Tìm phần thực và phần ảo của z.
b) Giải phương trình log2(x² + x + 2) = 3.
Câu 4 (1,0 điểm)
| 1 | ||
| Tính tích phân I = | ∫ | (x - 3)exdx |
| 0 |
Câu 5 (1,0 điểm). Trong không gian với hệ trục Oxyz, cho các điểm A (1; -2; 1), B(2; 1; 3) và mặt phẳng (P) x - y + 2z - 3 = 0. Viết phương trình đường thẳng AB và tìm tọa độ giao điểm của đường thẳng AB với mặt phẳng (P).
Câu 6 (1,0 điểm).
a, Tính giá trị của biểu thức P = (1 - 3cos2α)(2 + 3cos2α), biết sinα = 2/3.
b, Trong đợt phòng chống dịch MERS-CoV, Sở y tế thành phố đã chọn ngẫu nhiên 3 đội phòng chống dịch cơ động trong số 5 đội của Trung tâm y tế dự phòng thành phố và 20 đội của Trung tâm y tế cơ sở để kiểm tra công tác chuẩn bị. Tính xác suất để có ít nhất 2 đội của các Trung tâm y tế cơ sở được chọn.
Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ACBD là hình vuông cạnh a, SA vuông góc với mặt phẳmg (ABCD), góc giữa đường thẳng SC và mặt phẳng (ACBD) bằng 45o. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SB, AC.
Câu 8 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A. Gọi H là hình chiếu vuông góc của A trên cạnh BC; D là điểm đối xứng của B qua H; K là hình chiếu của vuông góc C trên đường thẳng AD. Giả sử H (-5;-5), K (9;-3) và trung điểm của cạnh AC thuộc đường thẳng: x - y + 10 = 0. Tìm tọa độ điểm A.
Câu 9 (1,0 điểm). Giải phương trình:
![]()
Câu 10 (1,0 điểm). Cho các số thực a, b, c thuộc đoạn [1,3] và thỏa mãn điều kiện a + b + c = 6. Tìm giá trị lớn nhất của biểu thức:
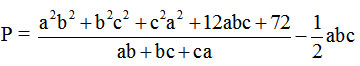
HẾT


