Đề thi chọn HSG thành phố môn Toán năm 2018 - 2019 Sở GD&ĐT Hải Phòng
Đề thi chọn HSG môn Toán có đáp án
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HẢI PHÒNG
(Đề thi gồm 01 trang)
KỲ THI CHỌN HỌC SINH GIỎI THÀNH PHỐ
CÁC MÔN VĂN HÓA CẤP THPT NĂM HỌC 2018 – 2019
ĐỀ THI MÔN:TOÁN – BẢNG B
Thời gian: 180 phút (không kể thời gian giao đề)
Ngày thi: 02/11/2018
Bài 1 (2,0 điểm)
a) Cho hàm số
32
3 91yx x x
=+ −+
có đồ thị là
( )
C
. Gọi
,
AB
là hai điểm cực trị của
(
)
.C
Tính
diện tích của tam giác
,OAB
trong đó
O
là gốc tọa độ.
b) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
2 46y x mx x=+ ++
có cực tiểu.
Bài 2 (2,0 điểm)
a) Giải phương trình
3
2sin sin cos 2
0.
tan 1
xx x
x
−+
=
−
b) Tìm tất cả các giá trị thực của tham số
m
để hệ phương trình
( )
32
2
22
3 12
x y x xy m
x xy m
−− −=
+ −=−
có nghiệm.
Bài 3 (2,0 điểm) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
.B
Biết
, 2; 2AB BC a AD a SA a= = = =
và vuông góc với mặt phẳng
( )
.ABCD
a) Tính cosin của góc giữa hai mặt phẳng
( )
SBC
và
( )
.SCD
b) Cho
M
là điểm nằm trên cạnh
SA
sao cho
( )
0 2.SM x x a= <<
Mặt phẳng
( )
BCM
chia khối
chóp thành hai phần có thể tích là
1
V
và
2
V
(trong đó
1
V
là thể tích của phần
chứa đỉnh
S
). Tìm
x
để
1
2
1
.
2
V
V
=
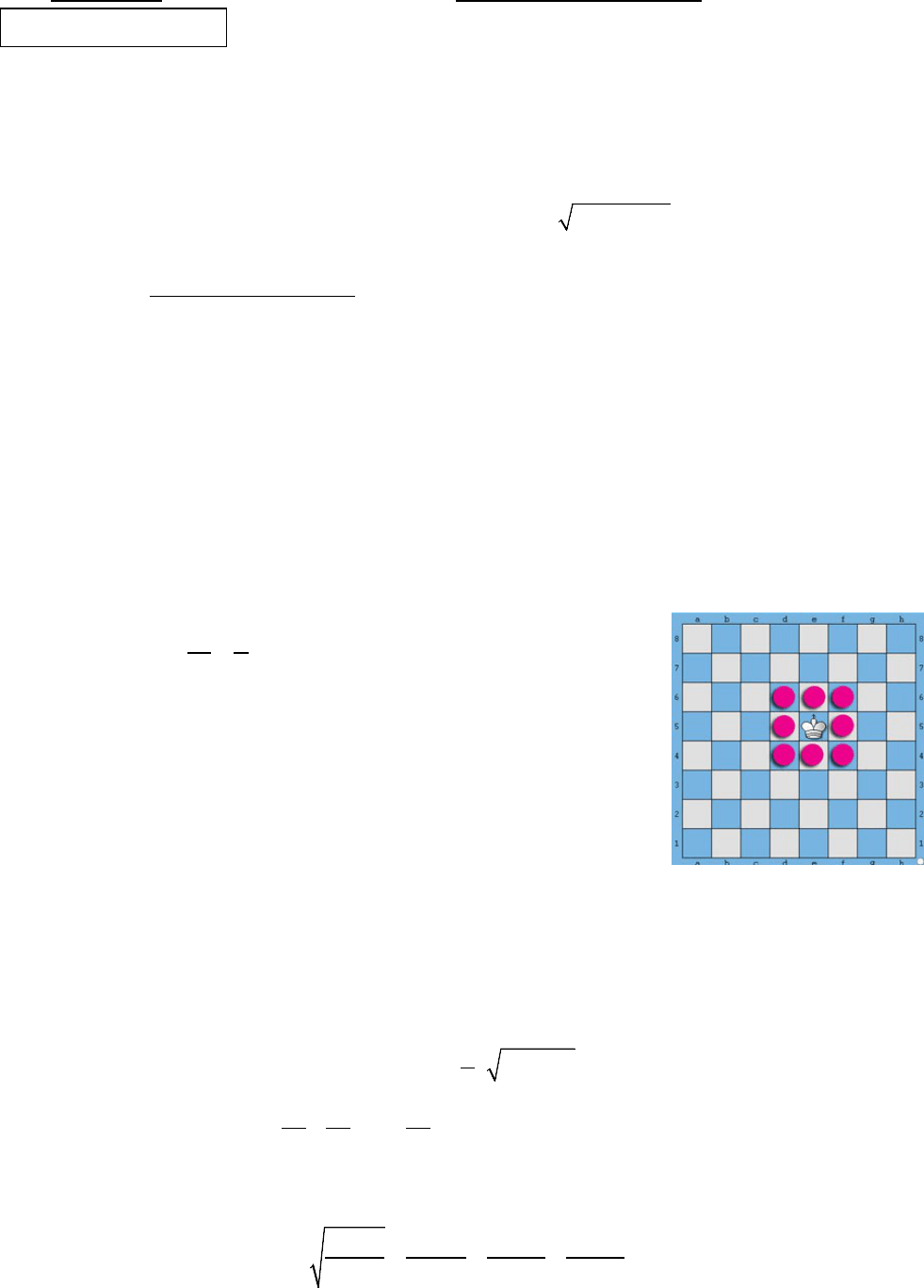
Bài 4 (1,0 điểm) Một quân vua được đặt trên một ô giữa bàn cờ vua. Mỗi
bước di chuyển, quân vua được chuyển sang một ô khác chung cạnh hoặc
chung đỉnh với ô đang đứng (xem hình minh họa). Bạn An di chuyển quân
vua ngẫu nhiên 3 bước. Tính xác suất để sau 3 bước đi quân vua trở về ô
xuất phát.
Bài 5 (1,0 điểm) Trong mặt phẳng với hệ tọa độ
,Oxy
cho hình vuông
ABCD
tâm
E
, gọi
G
là trọng tâm tam giác
.ABE
Điểm
( )
7; 2K −
thuộc đoạn
ED
sao cho
.GA GK=
Tìm tọa độ đỉnh
A
và viết phương trình cạnh
,AB
biết đường thẳng
AG
có phương trình
3 13 0xy−− =
và đỉnh
A
có hoành độ nhỏ hơn
4.
Bài 6 (1,0 điểm) Cho dãy số
{ }
n
u
xác định bởi
(
)
1
2
1
3
.
1
5 , ,1
2
n n nn
u
u u uun n
+
=
= ++ ∈ ≥
Ta thành lập dãy số
{ }
n
v
với
22 2
12
11 1
... .
n
n
v
uu u
= + ++
Chứng minh rằng dãy số
{ }
n
v
có giới hạn và
tính giới hạn đó.
Bài 7 (1,0 điểm) Cho các số thực dương
,,xyz
thỏa mãn điều kiện
2
; ;9 9x y x z x yz xz xy≥ > + ≤+
.
Tìm giá trị nhỏ nhất của biểu thức
3
9222yx yx yz zx
P
y xy yz xz
− +++
= +++
+ ++
.
……….HẾT……….
(Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh:............................................... Số báo danh:...............................................................
Cán bộ coi thi 1:................................................Cán bộ coi thi 2:............................................................
ĐỀ CHÍNH THỨC
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HẢI PHÒNG
(gồm 06 trang )
KỲ THI CHỌN HỌC SINH GIỎI THÀNH PHỐ
CÁC MÔN VĂN HÓA CẤP THPT NĂM HỌC 2018 – 2019
HƯỚNG DẪN CHẤM
ĐỀ THI MÔN:TOÁN – BẢNG KHÔNG CHUYÊN
Ngày thi: 02/11/2018
Bài Đáp án Điểm
Bài 1
(2.0 điểm)
a) Cho hàm số
32
3 91yx x x=+ −+
có đồ thị là
( )
C
. Gọi
,
AB
là hai điểm cực trị
của
(
)
.C
Tính diện tích của tam giác
,
OAB
trong đó
O
là gốc tọa độ.
1.00
+) Tập xác định
.D =
2
1
'3 6 9 '0
3
x
yxx y
x
=
= + −⇒ =⇔
= −
0.25
+)
(C) có hai điểm cực trị là
(
) (
)
3; 28 , 1; 4 .
AB−−
0.25
+)
( ) ( ) ( )
1
3; 28 , 1; 4 3. 4 1.28 8.
2
OAB
OA OB S=− = −⇒ =− −− =
0.50
b) Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
2 46y x mx x=+ ++
có
cực tiểu.
1.00
+) Tập xác định
;D =
2
2
'2
46
x
ym
xx
+
= +
++
.
Ta có: Hàm số có đạo hàm liên tục trên
nên hàm số có cực tiểu thì phương trình
’0y =
phải có nghiệm.
0.25
+) Xét phương trình
( )
2
2 46
'0 , 2
2
xx
ym x
x
− ++
= ⇔ = ≠−
+
.
Đặt
( )
{
}
2
2 46
, \2
2
xx
gx x
x
− ++
= ∈−
+
. Ta có:
(
)
(
)
2
2
4
' 0, 2
2 46
gx x
x xx
= > ∀ ≠−
+ ++
. Ngoài ra ta có
( ) (
)
lim 2; lim 2,
xx
gx gx
→+∞ →−∞
=−=
từ đó ta có bảng biến thiên của hàm số
( )
y gx=
như
sau:
Từ bảng biến thiên suy ra phương trình
’0y =
có nghiệm khi và chỉ
( ) ( )
; 2 2; .m∈ −∞ − ∪ +∞
0.25
+) Xét TH1:
2m >
Phương trình
’0y
=
có nghiệm duy nhất
0
x
, khi đó ta có:
lim ' 2 0; lim ' 2 0
xx
ym ym
→+∞ →−∞
=+> =−<
nên ta có bảng biến thiên của hàm số có dạng
0.25
x
– ∞
-2
+ ∞
y'
+
+
y
2
+ ∞
-2
– ∞
ĐÁP ÁN CHÍNH THỨC

2
Từ bảng biến thiên suy ra hàm số có cực tiểu.
+)TH2:
2m <−
Suy luận tương tự ta suy ra hàm số chỉ có cực đại, không thỏa mãn.
Vậy
2.m
>
Ghi chú: +) Nếu bài làm chỉ sử dụng điều kiện đủ: Hệ
( )
(
)
0
0
'0
'' 0
yx
yx
=
>
có nghiệm thì
trừ
0.25
điểm.
+) Nếu bài làm tìm điều kiện của
m
để pt
’0y =
có nghiệm và xét dấu
’’y
trong
hai trường hợp
2; 2mm> <−
thì cho điểm tối đa.
0.25
Bài 2
(1.0 điểm)
a) Giải phương trình
3
2sin sin cos2
0.
tan 1
xx x
x
−+
=
−
1.00
Điều kiện:
4
,.
2
xk
k
xk
π
π
π
π
≠+
∈
≠+
0.25
Với điều kiện trên phương trình đã cho tương đương với
( )
3
2
2
2sin sin cos 2 0 sin 1 cos2 0
42
xk
xx x x x
k
x
π
π
ππ
= +
−+ =⇔ − =⇔
= +
0.50
Kết hợp điều kiện đề bài thì phương trình có công thức nghiệm là
3
,.
4
x kk
π
π
=+∈
0.25
b) Tìm tất cả các giá trị thực của tham số
m
để hệ phương trình
( )
32
2
22
3 12
x y x xy m
x xy m
−− −=
+ −=−
có nghiệm.
1.00
+) Ta có:
( )
( )
( )
( )
( )
2
32
2
2
2
22
3 12
2 12
x x xy m
x y x xy m
x xy m
x x xy m
+ −=
−− −=
⇔
+ −=−
++ −=−
+) Đặt
2
;2a x xb x y=+=−
với điều kiện
2
1
.
4
ax x= + ≥−
0.25
Hệ đã cho có dạng
.
12
ab m
ab m
=
+=−
. Suy ra
,ab
là hai nghiệm của phương trình
( ) ( )
2
1 2 0*t mt m−− +=
.
Hệ ban đầu có nghiệm khi và chỉ khi phương trình (*) có nghiệm
1
.
4
t ≥−
0.25
x
– ∞
+ ∞
y
y'
0
-
+
Đề thi chọn HSG thành phố môn Toán năm 2018 - 2019
VnDoc xin giới thiệu tới bạn đọc Đề thi chọn HSG thành phố môn Toán năm 2018 - 2019 Sở GD&ĐT Hải Phòng. Tài liệu sẽ giúp các bạn học sinh giải bài tập Toán lớp 12 hiệu quả hơn. Mời các bạn học sinh tham khảo.