Đề thi học sinh giỏi lớp 12 THPT tỉnh Lào Cai môn Toán (năm học 2010 - 2011)
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ CHÍNH THỨC |
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 12 THPT ĐỀ THI MÔN: TOÁN |
Câu 1 (5,5 điểm)
1. Giải phương trình: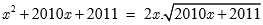 
2. Giải hệ phương trình: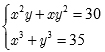 
Câu 2 (3,0 điểm)
Tìm tất cả các hàm số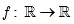 
thỏa mãn điều kiện 
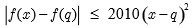với mọi số thực x và mọi số hữu tỷ q.
Câu 3 (6,0 điểm)
1. Trong mặt phẳng Oxy, chotam giác ABC có đỉnh A(5; 2), đường trung trực cạnh BC, đường trung tuyến kẻ từ đỉnh C của tam giác ABC lần lượt có phương trình là d: x + y - 6 = 0 và d': 2x - y + 3 = 0. Tìm tọa độ các đỉnh còn lại của tam giác ABC.
2. Cho hình chóp tam giác đều S.ABC, có cạnh đáy bằng a. Gọi α là góc giữa mặt bên và mặt đáy, β là góc giữa hai mặt bên kề nhau. Tính thể tích của hình chóp S.ABC và chứng minh rằng: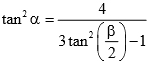 
Câu 4 (2,5 điểm)
Trong mặt phẳng cho n đường thẳng (n ≥ 3) trong đó không có hai đường thẳng nào song song và không có ba đường thẳng nào đồng quy. Chứng minh rằng tồn tại một tam giác được tạo thành từ ba đường thẳng đã cho mà tam giác này không bị chia cắt bởi bất kỳ đường thẳng nào trong các đường thẳng còn lại.
Câu 5 (3,0 điểm)
Với các chữ số 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số gồm bẩy chữ số khác nhau sao cho ba chữ số lẻ không đứng cạnh nhau.
