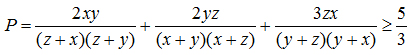Đề thi học sinh giỏi lớp 11 THPT tỉnh Quảng Bình môn Toán (năm học 2010 - 2011)

SỞ GIÁO DỤC VÀ ĐÀO TẠO QUẢNG BÌNH ĐỀ CHÍNH THỨC

KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 11 THPT NĂM HỌC 2010 – 2011 ĐỀ THI MÔN: TOÁN Thời gian làm bài: 180 phút (không kể thời gian phát đề)

Câu 1: (3.0 điểm)

a) Giải phương trình:

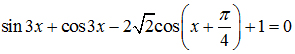
b) Giải hệ phương trình:

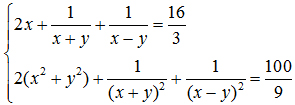
Câu 2: (2.0 điểm) Cho dãy số (x_n) xác định như sau:


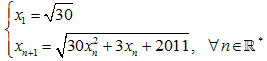
Tìm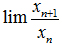

Câu 3: (3.0 điểm)
Cho tứ diện đều ABCD cạnh a. Gọi I, J lần lượt là trọng tâm các tam giác ABC và DBC. Mặt phẳng qua IJ cắt các cạnh AB, AC, DC, DB lần lượt tại các điểm M, N, P, Q với AM = x, AN = y (0 < x, y < a).

a) Chứng minh MN, PQ, BC đồng qui hoặc song song và MNPQ là hình thang cân.

b) Chứng minh rằng: a(x + y) = 3xy. Suy ra: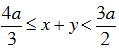

c) Tính diện tích tứ giác MNPQ theo a và s = x + y

Câu 4: (1.0 điểm) Cho phương trình: ax² + (2b + c)x + (2d + e) = 0 có một nghiệm không nhỏ hơn 4. Chứng minh rằng phương trình ax⁴ + ax³ + cx² + dx + e = 0có nghiệm.

Câu 5: (1.0 điểm) Cho x, y, z > 0. Chứng minh rằng: