Đề thi học sinh giỏi môn Toán lớp 9 thành phố Hải Phòng năm học 2016 - 2017

Đề thi học sinh giỏi môn Toán lớp 9

Đề thi học sinh giỏi môn Toán lớp 9 thành phố Hải Phòng năm học 2016 - 2017 có đáp án đi kèm là tài liệu tham khảo hay giúp các em ôn luyện và củng cố kiến thức, sẵn sàng cho kỳ thi học sinh giỏi lớp 9 THCS sắp tới.

Đề thi học sinh giỏi môn Toán lớp 9 thành phố Hà Nội năm học 2016 - 2017

Tuyển tập đề thi học sinh giỏi môn toán lớp 9

SỞ GIÁO DỤC & ĐÀO TẠO HẢI PHÒNG ĐỀ CHÍNH THỨC (Đề thi gồm 01 trang)

KỲ THI CHỌN HỌC SINH GIỎI THÀNH PHỐ CẤP THCS NĂM HỌC 2016 - 2017 ĐỀ THI MÔN: TOÁN Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi 12/4/2017

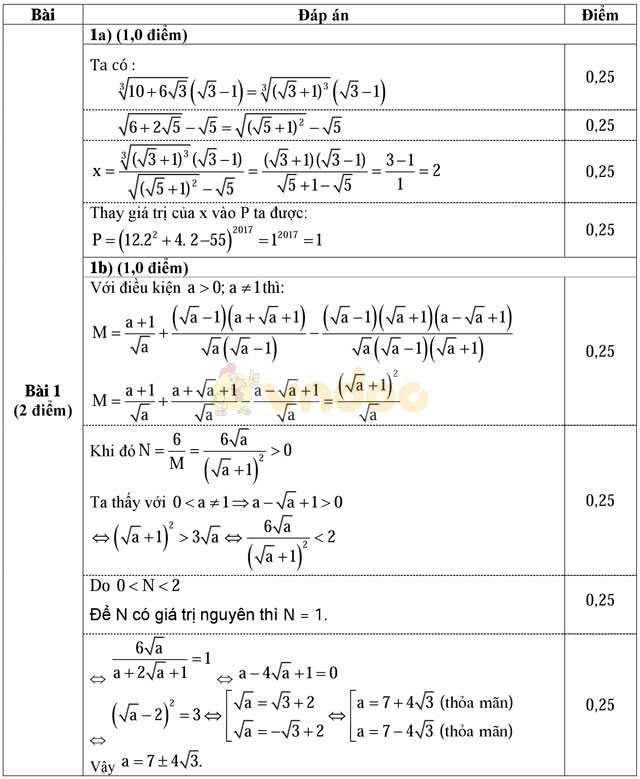
Bài 1. (2,0 điểm)

a) Cho 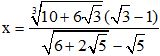. Tính giá trị của P = (12x² + 4x - 55)²⁰¹⁷..

b) Cho biểu thức 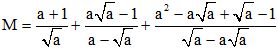với a > 0, a ≠ 1.

Với những giá trị nào của a thì biểu thức nhận giá trị nguyên?

Bài 2. (2,0 điểm)

a) Cho phương trình: x² - 2mx + m² - m - 6 (m là tham số). Với giá trị nào của m thì phương trình có hai nghiệm x₁ và x₂ sao cho |x₁| + |x₂| = 8?

b) Cho hệ phương trình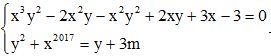

Tìm các giá trị của m để hệ phương trình có hai nghiệm phân biệt (x₂; y₁) và (x₂; y₂) thỏa mãn điều kiện (x₁ + y₂)(x₂ + y₁) + 3 = 0.

Bài 3. (2,0 điểm)

a) Tìm tất cả các số nguyên dương a, b sao cho a + b² chia hết cho a²b - 1.

b) Cho ba số thực a, b, c dương. Chứng minh rằng: .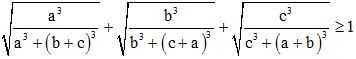

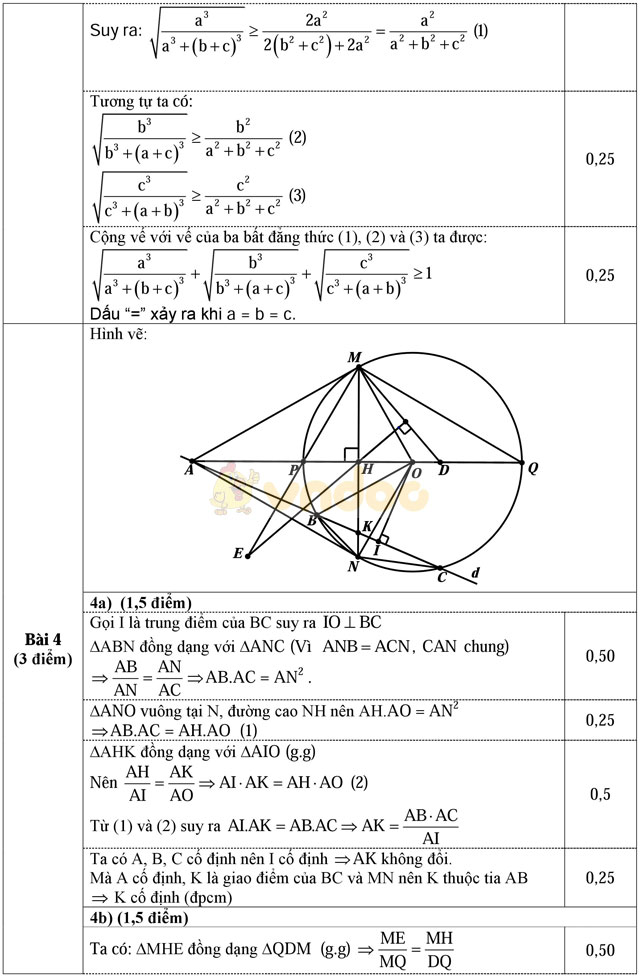
Bài 4. (3,0 điểm)

Cho ba điểm A, B, C cố định nằm trên một đường thẳng d (điểm B nằm giữa điểm A và điểm C). Vẽ đường tròn tâm O thay đổi nhưng luôn đi qua điểm B và điểm C (điểm O không thuộc đường thẳng d). Kẻ AM và AN là các tiếp tuyến với đường tròn tâm O (với M và N là các tiếp điểm). Đường thẳng BC cắt MN tại điểm K. Đường thẳng AO cắt MN tại điểm H và cắt đường tròn tại các điểm P và điểm Q (P nằm giữa A và Q).

a) Chứng minh điểm K cố định khi đường tròn tâm O thay đổi.

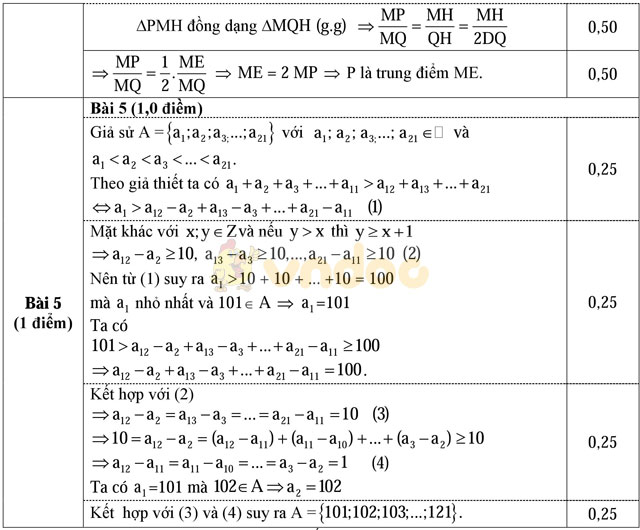
b) Gọi D là trung điểm của HQ, từ H kẻ đường thẳng vuông góc với MD cắt đường thẳng MP tại E. Chứng minh P là trung điểm của ME.

Bài 5. (1,0 điểm)

Cho tập hợp A gồm 21 phần tử là các số nguyên khác nhau thỏa mãn tổng của 11 phần tử bất kỳ lớn hơn tổng của 10 phần tử còn lại. Biết các số 101 và 102 thuộc tập hợp A. Tìm tất cả các phần tử của tập hợp A.

---------Hết---------
(Cán bộ coi thi không giải thích gì thêm)

Đáp án đề thi học sinh giỏi môn Toán lớp 9