Đề thi học sinh giỏi tỉnh Long An lớp 12 vòng 2 năm 2011 - 2012 môn Toán

Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi học sinh giỏi tỉnh Long An lớp 12 vòng 2 năm 2011 - 2012 môn Toán.

Đề thi học sinh giỏi môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO LONG AN (Đề thi chính thức)

KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 VÒNG II MÔN THI: TOÁN (Thời gian làm bài 180 phút không kể thời gian giao đề) Ngày thi: 10/11/2011

Bài 1 (4 điểm)

a) Giải phương trình:

b) Cho ba số thực dương a, b, c. Chứng minh:

Bài 2 (5 điểm)

Cho dãy số thực (x_n) với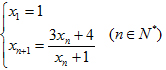

Xét các dãy số thực (u_n) với u_n = x_2n-1 (n thuộc N*) và (v_n) với v_n = x_2n (n thuộc N*)

a) Chứng minh các dãy số (u_n), (v_n) có giới hạn hữu hạn khi n -> +

b) Chứng minh các dãy số (x_n) có giới hạn hữu hạn khi n -> + và tìm giới hạn đó.

Bài 3 (5 điểm)

a) Cho tam giác có lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp. Gọi là điểm sao cho . Gọi G₁, G₂, G₃ lần lượt là trọng tâm các tam giác KBC, KCA, KAB

Chứng minh: G₁A, G₂B, G₃C đồng quy và G₁A = G₂B = G₃C

b) Trong mặt phẳng cho ngũ giác đều ABCDE nội tiếp đường tròn tâm O bán kính R và điểm tùy ý.Tìm vị trí của M để MA + MB + MC + MD + ME ngắn nhất.

Bài 4 (3 điểm)

Chứng minh rằng không tồn tại các số nguyên x, y, z sao cho: x²⁰¹² + 2009y²⁰¹² = 2011 + 2012z²⁰¹⁰

Bài 5 (3 điểm)

Trên mặt phẳng cho 2011 điểm sao cho với ba điểm bất kỳ trong số các điểm đó ta luôn tìm được hai điểm để đoạn thẳng được tạo thành có độ dài bé hơn 1. Chứng minh luôn tồn tại một hình tròn bán kính 1 chứa không ít hơn 1006 điểm đã cho.