Đề thi Olympic cụm trường THPT Ba Đình - Tây Hồ năm học 2011 - 2012 môn Toán lớp 11

Câu 1 (7 điểm):

a) Giải phương trình lượng giác:

b) Tính các giới hạn sau:

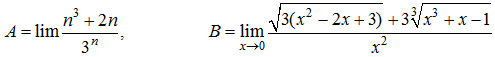
Câu 2 (4 điểm):

Cho dãy số (u_n), n thuộc R* xác định bởi: u₁ = 1, u₂ = 2 và u_n+2 - 2_un+1 + u_n = 2012 + a.n và với tham số a thuộc R.

a) Khi a = 0. Xét dãy số (v_n) với v_n = u_n+1 - u_n, n thuộc N*. Chứng minh rằng dãy số (v_n) là một cấp số cộng. Tính tổng 2012 số hạng đầu tiên của cấp số cộng đó.

b) Xác định số hạng tổng quát của dãy số (u_n).

Câu 3 (7 điểm):

Trong không gian, cho 3 tia Ox, Oy, Oz đôi một vuông góc với nhau. A, B, C lần lượt là các điểm di động trên các tia Ox, Oy, Oz sao cho: với k là một hằng số dương.

a) Chứng minh rằng tam giác ABC là tam giác nhọn và trực tâm H của tam giác ABC luôn cách O một khoảng không đổi.

b) Chứng minh rằng: lần lượt là diện tích các tam giác ABC, OAB, OBC, OCA.

c) M là điểm thuộc miền trong tam giác ABC (M không thuộc các cạnh của tam giác). Gọi α, β, γ lần lượt là các góc hợp bởi đường thẳng OM và các đường thẳng OA, OB, OC. Chứng minh rằng:

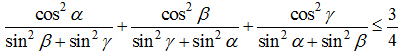
Câu 4 (2 điểm):

Cho dãy số (an) với n thuộc N*, gồm các số tự nhiên, được xác định như sau:

Với mỗi n thuộc N*, xét a_n + 1 điểm khác nhau cùng nằm trên một mặt phẳng, trong đó không có 3 điểm nào thẳng hàng. Mỗi đoạn thẳng nối hai trong a_n + 1 điểm này được tô bằng một trong n màu khác nhau. Chứng minh rằng, tồn tại tam giác có đỉnh là ba trong a_n + 1 điểm đã cho và các cạnh đều được tô cùng một màu.