Giải bài tập ôn tập cuối năm Hình học 12

Giải bài tập Toán 12 ôn tập cuối

Để giúp các bạn học sinh lớp 12 có kết quả cao trong học tập, VnDoc.com xin giới thiệu tới các bạn học sinh tài liệu: Giải bài tập ôn tập cuối năm Hình học 12, tài liệu bao gồm các bài tập trong SGK trang 99, 100, 101, 102 SGK kèm theo lời giải chi tiết sẽ giúp các bạn học sinh giải nhanh các bài tập Toán. Mời các bạn học sinh và thầy cô tham khảo.

Giải bài tập ôn tập cuối năm Hình học 12

Bài 1 (trang 99 SGK Hình học 12): Cho lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F'. O và O' là tâm đường tròn ngoại tiếp hai đáy, mặt phẳng (P) đi qua trung điểm của OO' và cắt các cạnh bên của lăng trụ. Chứng minh rằng (P) của lăng trụ đã cho thành hai đa diện có thể tích bằng nhau.

Lời giải:

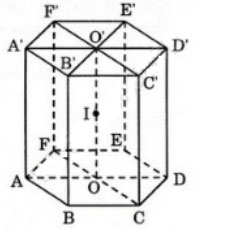
Gọi I là trung điểm của OO'

ABCDEF.A'B'C'D'E'F' là hình lăng trụ lục giác đều nên I là tâm đối xứng của các hình chữ nhật ADD'A', BEE'B', CFF'C'. Vậy nếu mp(P) đi qua I và cắt các cạnh AA', BB', CC', DD', EE', FF' theo thứ tự tại các điểm M, N, P, Q, R, S thì I là trung điểm của MQ, NR và PS

Suy ra phép đối xứng qua điểm I biến ABCDEF.MNPQRS thành D'E'F'A'B'C'.QRSMNP.

Nghĩa là ABCDEF.MNPQRS và D'E'F'A'B'C'. QRSMNP là hai khối da điện bằng nhau.

Vậy hai khối đa diện nói trên có thể tích bằng nhau.

Bài 2 (trang 99 SGK Hình học 12): Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi E và F lần lượt là trung điểm của B'C' và C'D'. Mặt phẳng (AEF) chia khối lập phương đó thành hai khối đa diện (H) và (H') trong đó (H) là khối đa diện chứa đỉnh A'. Tính thể tích của (H).

Lời giải:

Bài 3 (trang 99 SGK Hình học 12): Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó.

a) Thể tích của khối nón theo r và h.

b) Xác định h để thể tích của hình nón là lớn nhất.

Lời giải:

Bài 4 (trang 99 SGK Hình học 12): Trong không gian Oxyz cho hai điểm A(1; 2; -1), B(7; -2; 3) và đường thẳng d có phương trình

Lời giải

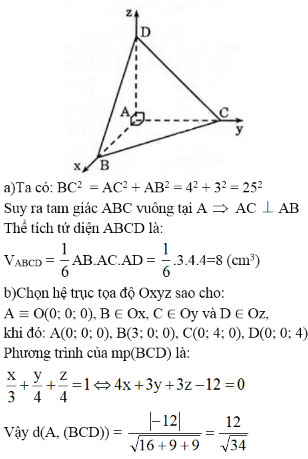
Bài 5 (trang 99 SGK Hình học 12): Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC). Biết rằng AC = AD = 4cm, AB = 3cm, BC = 5cm.

a) Tính thể tích tứ diện ABCD

b) Tính khoảng cách từ điểm A tới mặt phẳng (BCD)

Lời giải:

Bài 6 (trang 100 SGK Hình học 12): Trong không gian Oxyz, cho mặt cầu (S) có phương trình: x² + y² + z² = 4a² (a > 0).

a) Tính diện tích của mặt cầu (S) và thể tích của khối cầu tương ứng.

b) Mặt cầu (S) cắt mặt phẳng (Oxy) theo đường tròn (C). Xác định tâm và bán kính của (C).

c) Tính diện tích xung quanh của hình lăng trụ nhân (C) làm đáy và có chiều cao bằng a . Tính thể tích của khối trụ tương ứng.

Lời giải:

Bài 7 (trang 100 SGK Hình học 12): Trong không gian Oxyz cho hai đường thẳng:

Lời giải

Bài 8 (trang 100 SGK Hình học 12): Trong không gian Oxyz cho các điểm A(1; 0; -1), B(3; 4; -2), C(4; -1; 1), D(3; 0; 3)

a) Chứng minh rằng A, B, C, D không đồng phẳng

b) Viết phương trình mặt phẳng (ABC) và tính khoảng cách từ D đến (ABC).

c) Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD.

d) Tính thể tích tứ diện ABCD.

Lời giải:

Bài 9 (trang 100 SGK Hình học 12): Trong không gian Oxyz cho bốn điểm A(2; 4; -1), B (1; 4; -1), C(2; 4; 3), D(2; 2; -1)

a) Chứng minh rằng các đường thẳngAB, AC, AD vuông góc với nhau từng đôi một. Tính thể tích khối tứ diện ABCD.

b) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D

c) Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu (S) và song song với mp(ABD).

Lời giải:

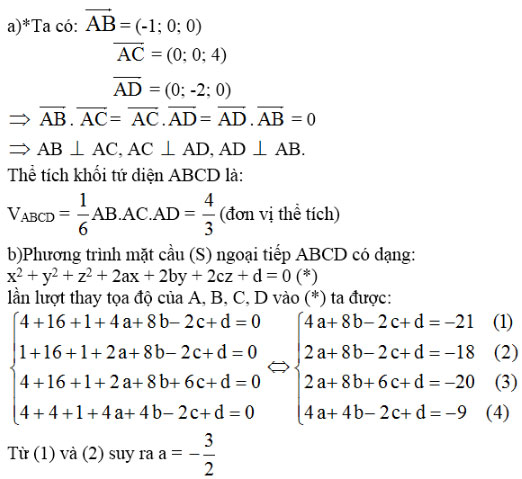
Bài 10 (trang 101 SGK Hình học 12): Trong không gian Oxyz cho đường thẳng ...

Lời giải

Bài 11 (trang 101 SGK Hình học 12): Trong không gian Oxyz cho các điểm A(-1; 2; 0); B(-3; 0; 2), C(1; 2; 3), D(0; 3; -2)

a) Viết phương trình mặt phẳng (ABC) và phương trình tham số của đường thẳng AD.

b) Viết phương trình mặt phẳng (α) chứa AD và song song với BC.

Lời giải:

Bài 12 (trang 101 SGK Hình học 12): Trong không gian Oxyz cho bốn điểm A(3; -2; -2), B(3; 2; 0), C(0; 2; 1) và D(-1; 1; 2)

a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện

b) Viết phương trình mặt cầu (S) tâm A và tiếp xúc với mặt phẳng (BCD)

c) Tìm tọa độ tiếp điểm của (S) và mặt phẳng (BCD)

Lời giải:

Bài 13 (trang 101 SGK Hình học 12): Trong không gian Oxyz cho hai đường thẳng ...

Lời giải

Bài 14 (trang 101 SGK Hình học 12): Trong không gian cho ba điểm A, B, C.

Lời giải

Bài 15 (trang 101 SGK Hình học 12): Cho hai đường thẳng chéo nhau:

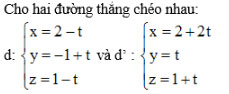
a) Viết phương trình các mặt phẳng (α) và ( β) song song với nhau và lần lượt chứa d và d'.

b) Lấy hai điểm M(2; -1; 1) và M'(2; 0; 1) lần lượt trên d và d'. Tính khoảng cách từ M đến mặt phẳng ( β) và khoảng cách từ M' đến mặt phẳng (α). So sánh hai khoảng cách đó.

Lời giải:

Bài 16 (trang 102 SGK Hình học 12): Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0

a) Chứng minh rằng (α) cắt ( β)

b) Viết phương trình tham số của đường thẳng d là giao của (α) và ( β)

c) Tìm điểm M' là ảnh của M(4; 2; 1) qua phép đối xứng qua mặt phẳng (α).

d) Tìm điểm N' là ảnh của N(0; 2; 4) quá phép đối xứng qua đường thẳng d.

Lời giải: