a) P + Q = (x2y + x3 – xy2 + 3) + (x3 + xy2 – xy – 6)
= x2y + x3 – xy2 + 3 + x3 + xy2 – xy – 6
= x2y+ (x3+ x3)+ (– xy2+ xy2)+( 3– 6) - xy
= x2y + 2x3 -3 - xy
b) M + N = (x2y + 0,5xy3 – 7,5x3y2 + x3) + (3xy2 – x2y + 5,5x3y2)
= x2y + 0,5xy3 – 7,5x3y2 + x3 + 3xy3 – x2y + 5,5x3y2
= (x2y – x2y) + (0,5xy3+ 3xy3) + (– 7,5x3y2+ 5,5x3y2) + x3
= 3,5xy3 – 2x3y2 + x3
Câu 2: Trang 46 sách toán VNEN 7 tập 2
Cho đa thức M = 3xyz – 3x2 + 5xy – 1 và N = 5x2 + xyz – 5xy + 3 – y
Tính M + N; M – N ; N – M
M + N = (3xyz – 3x2 + 5xy – 1) + (5x2 + xyz – 5xy + 3 – y)
= 3xyz – 3x2 + 5xy – 1 + 5x2 + xyz – 5xy + 3 – y
= (3xyz + xyz) + (– 3x2+ 5x2) + (5xy – 5xy) + (-1 +3) –y
= 4xyz + 2x2 – y + 2
M – N = (3xyz – 3x2 + 5xy – 1) – (5x2 + xyz – 5xy + 3 – y)
= 3xyz – 3x2 + 5xy – 1 - 5x2 - xyz + 5xy - 3 + y
= (3xyz- xyz) – (3x2 + 5x2) + (5xy + 5xy) – (1+3) + y
= 2xyz – 8x2 + 10xy + y – 4
N – M = (5x2 + xyz – 5xy + 3 – y ) – (3xyz – 3x2 + 5xy – 1)
= 5x2 + xyz – 5xy + 3 – y - 3xyz + 3x2 - 5xy + 1
= (5x2+ 3x2 ) + (xyz- 3xyz) – (5xy + 5xy) – y +( 3+ 1)
= 8x2 – 2xyz – 10xy – y + 4
Câu 3: Trang 46 sách toán VNEN 7 tập 2
Tìm đa thức P và đa thức Q biết:
a) P + (x2 – 2y2) = x2 – y2 + 3y2 – 1
b) Q – (5x2 – xyz) = xy + 2x2 – 3xyz + 5
a) P + (x2 – 2y2) = x2 – y2 + 3y2 – 1
=> P = (x2 – y2 + 3y2 – 1) – (x2 – 2y2)
=> P = x2 – y2 + 3y2 – 1 – x2 + 2y2
=> P = (x2 – x2) + (-y2 + 3y2 + 2y2) – 1
=> P = 4y2 – 1
b) Q – (5x2 – xyz) = xy + 2x2 – 3xyz + 5
=> Q = (xy + 2x2 – 3xyz + 5) + (5x2 – xyz)
=> Q = xy + 2x2 – 3xyz + 5 + 5x2 – xyz
=> Q = xy + (2x2 + 5x2) – (3xyz + xyz) + 5
=> Q = xy + 7x2 – 4xyz + 5
Câu 4: Trang 46 sách toán VNEN 7 tập 2
Tính giá trị của mỗi đa thức trong các trường hợp sau:
a) x2 + 2xy – 3x3 + 2y3 + 3x3 – y3 tại x = 5 và y = 4
b) xy – x2y2 + x4y4 – x6y6 + x8 y8 tại x = -1 và y = -1
a) x2 + 2xy – 3x3 + 2y3 + 3x3 – y3
= x2 + 2xy + (– 3x3+ 3x3) + (2y3– y3)
= x2 + 2xy + y3
Giá trị của đa thức x2 + 2xy + y3 tại x = 5 và y = 4 là: 52 + 2.5.4 + 43 = 129
b) Giá trị của đa thức xy – x2y2 + x4y4 – x6y6 + x8 y8 tại x = -1 và y = -1 là :
(-1).(-1) – (-1)2.(-1)2 + (-1)4.(-1)4 - (-1)6.(-1)6 + (-1)8.(-1)8
= 1 – 1 + 1 -1 + 1 = 1
Câu 5: Trang 46 sách toán VNEN 7 tập 2
Cho đa thức: A = x2 – 2y + xy + 1 ; B = x2 + y – x2y2 – 1
Tìm đa thức C sao cho a) C = A + B b) C + A = B
a) A + B = x2 – 2y + xy + 1 + (x2 + y – x2y2 – 1)
= x2 – 2y + xy + 1 + x2 + y – x2y2 – 1
= (x2 + x2 ) + ( -2y + y) + xy – x2y2 + (1 – 1)
= 2x2 – y + xy – x2y2.
Vậy thức C là 2x2 – y + xy – x2y2
b) C = B – A
= (x2 + y – x2y2 – 1) – (x2 – 2y + xy + 1)
= x2 + y – x2y2 – 1 - x2 + 2y - xy – 1
= (x2 – x2) + (y + 2y) – x2y2- xy – (1 + 1)
= 3y – x2y2- xy – 2.
Vậy đa thức C là 3y – x2y2- xy – 2.
Câu 6: Trang 46 sách toán VNEN 7 tập 2
Cho đa thức Q = - x2y5 + 3y2 – 3x3 + x3y + 2015 . Tìm một đa thức P sao cho tổng của P và Q là một đa thức không
P + Q = 0 => P = - Q
=> P = - (- x2y5 + 3y2 – 3x3 + x3y + 2015) = x2y5 - 3y2 + 3x3 - x3y – 2015
D.E. Hoạt động vận dụng và tìm tòi, mở rộng
Câu 1: Trang 47 sách toán VNEN 7 tập 2
Viết hai đa thức bất kì rồi tìm tổng và hiệu của chúng
A = x2 – 2y + 4xy + y2
B = - 4x2 – 2x – 4xy – y2 + 1
A + B = (x2 – 2y + 4xy + y2) + (- 4x2 – 2x – 4xy – y2 + 1)
= x2 – 2y + 4xy + y2 - 4x2 – 2x – 4xy – y2 + 1
= (x2 - 4x2) + (4xy– 4xy) + (y2 – y2) – 2y – 2x + 1
= -3x2 – 2y – 2x + 1
A – B = (x2 – 2y + 4xy + y2) - (- 4x2 – 2x – 4xy – y2 + 1)
= x2 – 2y + 4xy + y2 + 4x2 + 2x + 4xy + y2 - 1
= (x2 + 4x2) + (4xy+ 4xy) + (y2 + y2) – 2y + 2x - 1
= 5x2 +8xy + 2y2 – 2y – 2x + 1
Câu 2: Trang 47 sách toán VNEN 7 tập 2
Hình 5 mô tả cách mà em có thể làm để có một cái hộp có ba kích thước là x, y, z. Các kích thước và tỉ lệ hộp phụ thuộc vào các giá trị x, y, z. Viết và thu gọn biểu thức biểu thị cho diện tích các mặt của hình hộp được thể hiện qua hình đó.

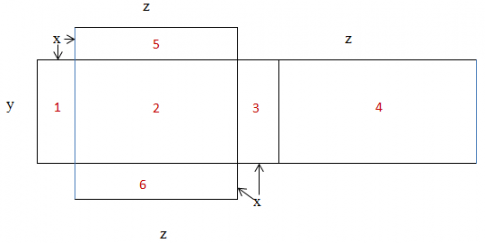
Đánh số các mặt từ 1 đến 6:
- S1 = S3 = x.y
- S2 = S4 = y.z
- S5 = S6 = x.z
=>Tổng diện tích các mặt là xy + yz + xz.
Câu 3: Trang 47 sách toán VNEN 7 tập 2
Cho đa thức sau:
M = 7x2y2 – 2xy – 5y3 – y2 + 5x4
N = -x2y2 – 4xy + 3y3 – 3y2 + 2x4
P = -3x2y2 + 6xy + 2y3 +6y2 + 7
Tính M + N + P. Từ đó hãy chứng minh rằng: ít nhất một trong ba đa thức đã cho có giá trị dương với mọi x, y.
M + N + P = (7x2y2 – 2xy – 5y3 – y2 + 5x4) + (-x2y2 – 4xy + 3y3 – 3y2 + 2x4) + (-3x2y2 + 6xy + 2y3 +6y2 + 7)
=7x2y2 – 2xy – 5y3 – y2 + 5x4 -x2y2 – 4xy + 3y3 – 3y2 + 2x4 -3x2y2 + 6xy + 2y3 +6y2 + 7
= (7x2y2-x2y2-3x2y2) + (– 2xy– 4xy+ 6xy) + (– 5y3 + 3y3 + 2y3) + (– y2– 3y2 +6y2) + (5x4+ 2x4) + 7
= 3x2y2 + 2y2 + 6x4 + 7
Ta thấy: x2y2 ≥ 0 với mọi x, y => 3x2y2 ≥ 0 với mọi x, y
y2 ≥ 0 với mọi y =>2y2 ≥ 0 với mọi y.
x4 ≥ 0 với mọi x =>6x4 ≥ 0 với mọi x.
=> M + N + P > 0 với mọi x, y => ít nhất một trong ba đa thức đã cho có giá trị dương với mọi x, y.
Ngoài Giải VNEN Toán 7 bài 5: Cộng, trừ đa thức, mời các bạn tham khảo thêm: Giải bài tập Toán lớp 7, Giải Vở BT Toán 7, Đề thi học kì 1 lớp 7, Đề thi giữa kì 1 lớp 7, Đề thi học kì 2 lớp 7... được cập nhật liên tục trên VnDoc.com.







