Giải Toán 7 VNEN Bài 8: Nghiệm của đa thức một biến

Giải Toán 7 VNEN bài Nghiệm của đa thức một biến được giới thiệu trên VnDoc.com. Đây là tài liệu được biên soạn theo chương trình VNEN Toán 7, sẽ giúp học sinh tiếp thu bài nhanh và hứng thú với bài học hơn.

Giải Toán 7 VNEN Bài 8: Nghiệm của đa thức một biến - Sách hướng dẫn học Toán 7 tập 2 trang 57, 58 nằm trong bộ VNEN của chương trình mới. Tài liệu bao gồm hướng dẫn trả lời và giải các bài tập trong bài học. Cách giải chi tiết, dễ hiểu, giúp các em học sinh nắm kiến thức nhanh chóng và dễ dàng.

A. Hoạt động khởi động

B. Hoạt động hình thành kiến thức

1.

a) Xét đa thức P(x) = 2x +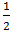

- Tính P(- )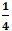

c) Thực hiện theo yêu cầu

- Giải thích tại sao x = - 1 và x = 1 là các nghiệm của đa thức Q(x) = x² – 1.

- Kiểm tra xem x = 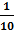có phải là nghiệm của đa thức P(x) = 5x + 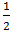hay không.

- Nếu cách kiểm tra một số a có phải là nghiệm của đa thức P(x) không.

- Giải thích tại sao đa thức G(x) = x² + 3 không có nghiệm.

Trả lời:

a)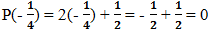

c) - Ta có: Q(-1) = (-1)² – 1 = 0

và Q(1) = (1)² – 1 = 0

Vì tại x = -1 và x = 1, đa thức Q(x) có giá trị bằng 0 nên chúng là các nghiệm của đa thức Q(x).

- Thay x = 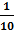vào đa thức P(x) = 5x + 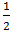ta được:

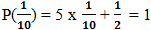(khác 0) suy ra x = 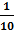không phải là nghiệm của đa thức P(x).

- Để kiểm tra một số a có phải là nghiệm của đa thức P(x) không, ta đi tìm P(a).

+ Nếu P(a) = 0 thì x = a là nghiệm của P(x)

+ Nếu P(a) khác 0 thì x = a không là nghiệm của P(x).

- Đa thức G(x) = x² + 3 không có nghiệm, vì tại x = b bất kỳ, ta luôn có:

G(b) = b² + 3 >= 0 + 3 > 0

2. Chú ý

b) Thực hiện theo yêu cầu

* x = - 2; x = 0 và x = 2 có phải là nghiệm của đa thức x³ – 4x hay không? Vì sao?

* Trong các số cho ở bảng sau, số nào là nghiệm của đa thức (ở cùng hàng)

Trả lời:

* Ta có:

- Thay x = - 2 vào đa thức x³ – 4x ta được (-2)³ – 4(-2) = 0

- Thay x = 0 vào đa thức x³ – 4x ta được (0)³ – 4(0) = 0

- Thay x = 2 vào đa thức x³ – 4x ta được (2)³ – 4(2) = 0

Vậy x = -2; x = 0 và x = 2 là các nghiệm của đa thức x³ – 4x.

* a) x = -1/4 là nghiệm của đa thức P(x) = 2x + ½

b) x = 3 và x = -1 là các nghiệm của đa thức Q(x) = x² – 2x – 3

Kết luận: Có thể tìm nghiệm của đa thức bằng cách tìm các giá trị của biến sao cho tại giá trị đó, giá trị của đa thức bằng 0.

C. Hoạt động luyện tập

Câu 1: Trang 57 sách VNEN Toán 7 tập 2

Kiểm tra xem mỗi số x = 1; x = 3 có phải là một nghiệm của đa thức sau không.

P(x) = x² – 4x + 3

Trả lời:

- Tại x = 1, đa thức P(x) có giá trị là: P(1) = (1)² – 4(1) + 3 = 0

- Tại x = 3, đa thức P(x) có giá trị là: P(3) = (3)² – 4(3) + 3 = 0

Vậy x = 1; x = 3 là một nghiệm của đa thức P(x)

Câu 2: Trang 57 sách VNEN Toán 7 tập 2

Trong tập hợp các số {1; 2; -1; 0}, số nào là nghiệm, số nào không phải là nghiệm của đa thức: R(x)= x⁴ + 2x³ – x² + x – 3?

Trả lời:

- Xét: R(1) = (1)⁴ + 2(1)³ – (1)² + 1 – 3 = 0

R(2) = (2)⁴ + 2(2)³ – (2)² + 2 – 3 = 27

R(1) = (-1)⁴ + 2(-1)³ – (-1)² + (-1) – 3 = - 6

R(1) = (0)⁴ + 2(0)³ – (0)² + 0 – 3 = - 3

Vậy tại x = 1, giá trị của đa thức R(x) = 0, nên x = 1 là nghiệm của đa thức R(x).

Tại x = 2, x = -1 và x = 0, giá trị của đa thức R(x) khác 0, nên chúng không phải là nghiệm của đa thức R(x).

Câu 3: Trang 57 sách VNEN Toán 7 tập 2

a) Tìm nghiệm của mỗi đa thức sau:

- P(y) = 3y – 6; - N(x) = 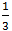– 2x; - D(z) = z³ - 27

- M(x) = x² – 4; - C(y) = √2y + 3

b) Chứng tỏ rằng đa thức sau không có nghiệm: Q(x) = x⁴ + 1

Trả lời:

a) Ta có:

- P(y) = 0 ⇔ 3y – 6 = 0 ⇔ 3y = 6 ⇔ y = 2

Vậy S = {2}

- N(x) = 0 ⇔ 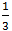– 2x = 0 ⇔ 2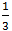x = ⇔ x =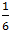

Vậy S = {}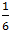

- D(z) = 0 ⇔ z³ - 27 = 0 ⇔ z³ = 27 ⇔ z = 3

Vậy S = {3}

- M(x) = 0 ⇔ x² – 4 = 0 ⇔ x² = 4 ⇔ x = 2 và x = -2

Vậy S = {2; -2}

- C(y) = 0 ⇔ √2y + 3 = 0 ⇔ √2y = -3 ⇔ y =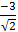

Vậy S= {}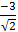

b) Tại x = a bất kỳ, ta luôn có: Q(a) = (a⁴) + 1 ≥ 0 + 1 > 0

Do đó tại x = a bất kỳ, giá trị của đa thức Q(x) luôn lớn hơn 0. Vậy đa thức Q(x) không có nghiệm.

D. Hoạt động vận dụng

Câu 1: Trang 57 sách Toán VNEN 7 tập 2

Bạn Hùng nói: "Ta chỉ có thể viết được một đa thức

một biến có nghiệm bằng 1"

Bạn Sơn nói: "Có thể viết được nhiều đa thức một biết có nghiệm bằng 1"

Ý kiến em thế nào?

Trả lời:

Em đồng ý với ý kiến của bạn Sơn.

Ta có thể viết được nhiều đa thức một biến có nghiệm bằng 1 với nhiều bậc khác nhau, ví dụ như:

M(x) = x - 1; N(x) = x² – 4x + 3; P(x) = x⁴ + 2x³ – x² + x – 3 ...

Câu 2: Trang 58 sách Toán VNEN 7 tập 2

Hãy viết một đa thức sao cho nó:

a) Có một nghiệm duy nhất là x = -3

b) Chỉ có 2 nghiệm là x = 2 và x = -2

c) Không có nghiệm

Trả lời:

a) Đa thức có một nghiệm duy nhất là x = -3: P(x) = x³ + 27

b) Đa thức chỉ có 2 nghiệm x = 2 và x = -2: F(x) = x² – 4

c) Đa thức không có nghiệm: K(x) = x⁴ + 5

E. Hoạt động tìm tòi mở rộng

Câu 1: Trang 58 sách Toán VNEN 7 tập 2

Cho đa thức A(x) = ax² + bx + c (với a, b, c là các hằng số). Chứng minh rằng:

a) Nếu a + b + c = 0 thì x = 1 là một nghiệm của đa thức A(x);

b) Nếu a – b + c = 0 thì x = -1 là một nghiệm của đa thức A(x);

Trả lời:

a) Giả sử x = 1 là một nghiệm của đa thức A(x), ta có:

A(1) = 0 ⇔ a(1)² + b(1) + c = 0 ⇔ a + b + c = 0 (đpcm)

Vậy a + b + c = 0 thì x = 1 là 1 nghiệm của đa thức A(x)

b) Giả sử x = -1 là nghiệm của đa thức A(x), ta có:

A(-1) = 0 ⇔ a(-1)² + b(-1) + c = 0 ⇔ a – b + c = 0 (đpcm)

Vậy a – b + c = 0 thì x = -1 là 1 nghiệm của đa thức A(x)

Câu 2: Trang 58 sách Toán VNEN 7 tập 2

Cho hai đa thức P(x) và Q(x) đều có nghiệm. Có thể khẳng định được rằng đa thức P(x) + Q(x) luôn có nghiệm hay không? Minh họa cho câu trả lời của em bằng một ví dụ.

Trả lời:

Có thể khẳng định được rằng đa thức P(x) + Q(x) luôn có nghiệm với P(x) và Q(x) đều có nghiệm.

Ví dụ: P(x) = 2x + 2 có nghiệm là x = -1

Và Q(x) = 3x – 6 có nghiệm là x= 2

Ta có P(x) + Q(x) = (2x + 1) + (3x – 6) = 5x – 5

- Xét F(x) = 5x – 5:

F(x) = 0 ⇔ 5x – 5 = 0 ⇔ x = 1

Vậy x = 1 là nghiệm của đa thức F(x) hay nói cách khác x =1 là nghiệm của đa thức P(x) + Q(x) (đpcm)

Câu 3: Trang 58 sách Toán VNEN 7 tập 2

Cho hai đa thức M(x) và N(x) có cùng một nghiệm. Có thể khẳng định được rằng đa thức M(x) + N(x) luôn có nghiệm hay không? Cho một ví dụ minh họa cho câu trả lời của em.

Trả lời:

Có thể khẳng định được rằng đa thức M(x) + N(x) luôn có nghiệm với M(x) và N(x) có cùng một nghiệm.

Ví dụ: M(x) = 4x + 8 có nghiệm là x = -2

Và N(x) = 3x + 6 có nghiệm là x = -2

Ta có M(x) + N(x) = (4x + 8) + (3x + 6) = 7x +14

- Xét F(x) = 7x + 14:

F(x) = 0 ⇔ 7x + 14 = 0 ⇔ x = -2

Vậy x = - 2 là nghiệm của đa thức F(x) hay nói cách khác x = -2 là nghiệm của đa thức M(x) + N(x) với M(x) và N(x) có cùng một nghiệm. (đpcm)

Ngoài Giải Toán 7 VNEN Bài 8: Nghiệm của đa thức một biến, mời các bạn tham khảo thêm: Giải bài tập Toán lớp 7, Giải Vở BT Toán 7, Đề thi học kì 1 lớp 7, Đề thi giữa kì 1 lớp 7, Đề thi học kì 2 lớp 7... được cập nhật liên tục trên VnDoc.com.