a) P(x) = 2 + 3x2 – 3x3 + 5x4 – 2x – x3 + 7x5.
= 2 + 3x2 + (– 3x3 – x3) + 5x4 – 2x+ 7x5
= 2 + 3x2 – 4x3 + 5x4 – 2x+ 7x5
Sắp xếp theo lũy thừa giảm dần:
P(x) = 7x5 + 5x4 – 4x3 + 3x2 – 2x + 2.
b) 7 là hệ số của lũy thừa bậc 5;
5 là hệ số của lũy thừa bậc 4;
-4 là hệ số của lũy thừa bậc 3;
3 là hệ số của lũy thừa bậc 2
-2 là hệ số của lũy thừa bậc 1
2 là hệ số của lũy thừa bậc 0.
Câu 2: Trang 51 sách toán VNEN 7 tập 2
Cho đa thức Q(x) = 2x4 + 4x3 – 5x6 – 4x – 1
a) Sắp xếp các hạng tử của đa thức Q(x) theo lũy thừa giảm dần của biến;
b) Viết đa thức Q(x) đầy đủ lũy thừa bậc cao nhất đến lũy thừa bậc 0.
a) Sắp xếp Q(x) theo lũy thừa giảm dần của biến:
Q(x) = – 5x6 + 2x4 + 4x3 – 4x – 1
b) Q(x) = – 5x6 +0x5 + 2x4 + 4x3 + 0x2 – 4x – 1
Câu 3: Trang 47 sách toán VNEN 7 tập 2
Tính giá trị của đa thức P(x) = x2 – 6x + 9 tại mỗi giá trị sau: x = 3; x = -3
Với x = 3: P(3) = 32 – 6.3 + 9 = 0
Với x = -3: P(-3) = (-3)2 – 6.(-3) + 9 = 36
Câu 4: Trang 51 sách toán VNEN 7 tập 2
Trong mỗi trường hợp sau đây, số nào trong ba số được cho ở bên phải là bậc của đa thức đã cho ? Khoanh vào số mà em chọn.
|
a) 5x2 – 2x3 + x4 – 3x2 – 5x5 + 1 |
-5 |
5 |
4 |
|
b) 15 – 2x |
15 |
-2 |
1 |
|
c) 3x5 + x3 – 3x5 + 1 |
3 |
5 |
1 |
|
d) - 1 |
1 |
-1 |
0 |
a) 5x2 – 2x3 + x4 – 3x2 – 5x5 + 1
Bậc cao nhất là bậc 5 (5x5) => Bậc của đa thức là 5.
b) 15 – 2x
Bậc cao nhất là bậc 1 (2x) => Bậc của đa thức là 1.
c) 3x5 + x3 – 3x5 + 1 = (3x5– 3x5) + x3 + 1 = x3 + 1
Bậc cao nhất là bậc 3 (x3) => Bậc của đa thức là 3.
d) – 1
Bậc cao nhất là bậc 0 (-1) => Bậc của đa thức là 0.
Câu 5: Trang 51 sách toán VNEN 7 tập 2
Tính giá trị của mỗi đa thức sau tại giá trị của biến đã chỉ ra:
a) x2 + x4 + x6 + x8 + … + x100 tại x = -1
b) ax2 + bx + c tại x = -1; x = 1 (a, b, c là hằng số)
Trả lời:
a) x2 + x4 + x6 + x8 + … + x100 = (-1)2 + (-1)4 + (-1)6 + (-1)8 + … + (-1)100
= 1 + 1 + 1 + 1 +… + 1
Số hạng tử “1” trong biểu thức trên là  +1 = 50 (hạng tử)
+1 = 50 (hạng tử)
⇒ Giá trị của x2 + x4 + x6 + x8 + … + x100 khi x = -1 là 50.1 = 50
b) Tại x = -1 ⇒ ax2 + bx + c = a(-1)2 + b(-1) + c = a –b + c
Tại x = 1 ⇒ ax2 + bx + c = a.12+ b.1 + c = a + b + c.
D. Hoạt động vận dụng
Câu 1: Trang 51 sách toán VNEN 7 tập 2
Viết một đa thức một biến có hai hạng tử mà hệ số cao nhất là 5 còn hệ số tự do là -1.
A = xy2 – 2x2 + 5x3y2 – 1
B = xy – 4x2y2 + y2 + x4y – 1
…
Giải câu 2 trang 51 sách toán VNEN lớp 7 tập 2
a) Viết các đa thức một biến có bậc là 10. Em viết được bao nhiêu đa thức như thế trong thời gian 5 phút.
b) Hãy sắp xếp các đa thức đã viết được trong câu a) theo lũy thừa tăng hoặc giảm của biến; chỉ rõ hệ số cao nhất, hệ số tự do của mỗi đa thức đó.
a) Một sô đa thức một biến có bậc là 10:
A = 4x10 + x -1; B = 2x10 – x + 2; C = 3x10 + 2x + 2; D = 3x10 + 2; E = 4x10 + x
F = 2x10 – 3x + 2; G = 3x10 + x2y + x,…
b) A = 4x10 + x -1 => Hệ số của lũy thừa bậc cao nhất (10) là 4, hệ số tự do là -1.
B = 2x10 – x + 2; => Hệ số của lũy thừa bậc cao nhất (10) là 2, hệ số tự do là 2.
C = 3x10 + 2x + 2; => Hệ số của lũy thừa bậc cao nhất (10) là 3, hệ số tự do là 2.
D = 3x10 + 2; => Hệ số của lũy thừa bậc cao nhất (10) là 3, hệ số tự do là 2.
E = 4x10 + x => Hệ số của lũy thừa bậc cao nhất (10) là 4, hệ số tự do là 0
F = 2x10 – 3x + 2; => Hệ số của lũy thừa bậc cao nhất (10) là 2, hệ số tự do là 2.
G = 3x10 + x2y + x => Hệ số của lũy thừa bậc cao nhất (10) là 2, hệ số tự do là 0.
Câu 3: Trang 51 sách toán VNEN 7 tập 2
Viết dạng tổng quát của đa thức bậc ba biến x theo lũy thừa giảm dần của biến.
Dạng tổng quát: ax3 + bx2 + cx + d ( với a, b, c, d là hệ số và a ≠ 0)
Ngoài Giải VNEN Toán 7 bài 6: Đa thức một biến, mời các bạn tham khảo thêm: Giải bài tập Toán lớp 7, Giải Vở BT Toán 7, Đề thi học kì 1 lớp 7, Đề thi giữa kì 1 lớp 7, Đề thi học kì 2 lớp 7... được cập nhật liên tục trên VnDoc.com.
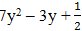 và B =
và B = 
 .
.






