Lý thuyết vật lý 10 Bài tập cuối chương 2 KNTT

Sách Kết nối tri thức

1 24

Chúng tôi xin giới thiệu bài Lý thuyết Vật lý lớp 10 Bài tập cuối chương 2 được VnDoc sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Vật lý lớp 10 sách Kết nối tri thức. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

Bài tập cuối chương 2

A. Lý thuyết Vật lý 10 bài tập cuối chương 2
B. Bài tập minh họa

A. Lý thuyết Vật lý 10 bài tập cuối chương 2

1. Độ dịch chuyển và quãng đường đi được

- Độ dịch chuyển là một đại lượng vecto, cho biết độ dài và hướng của sự thay đổi vị trí của vật.

- Khi vật chuyển động thẳng, không đổi chiều thì độ lớn của độ dịch chuyển và quãng đường đi được bằng nhau. Khi vật chuyển động thẳng, có đối chiếu thì độ lớn của độ dịch chuyển và quãng đường đi được không bằng nhau.

- Tổng hợp các độ dịch chuyển bằng cách tổng hợp vecto.

2. Tốc độ và vận tốc

- Tốc độ trung bình trên một đoạn đường xác định (hoặc trong một khoảng thời gian xác định):

$v = \frac{S}{t}$ hoặc $v = \frac{{\Delta S}}{{\Delta t}}$

- Tốc độ tức thời là tốc độ tại một thời điểm xác định.

- Vận tốc trung bình trên một độ dịch chuyển xác định (hoặc trong một khoảng thời gian xác định):

$\overrightarrow v = \frac{{\overrightarrow d }}{t}$ hoặc $\overrightarrow v = \frac{{\Delta \overrightarrow d }}{{\Delta t}}$

- Vận tốc tức thời là vận tốc tại một điểm xác định:

${\overrightarrow v _t} = \frac{{\Delta \overrightarrow d }}{{\Delta t}}$ với Δt rất nhỏ.

- Khi vật chuyển động thẳng theo một hướng thì tốc độ và vận tốc có độ lớn bằng nhau: v= v

- Công thức cộng vận tốc: ${\overrightarrow v _{1,3}} = {\overrightarrow v _{1,2}} + {\overrightarrow v _{2,3}}$

Trong đó:

${\overrightarrow v _{1,2}}$ là vận tốc của vật (1) đối với vật (2);

${\overrightarrow v _{2,3}}$ là vận tốc của vật (2) so với vật (3) đứng yên;

${\overrightarrow v _{1,3}}$ (vận tốc tổng hợp của vật) là vận tốc của vật (1) đối với vật (3)

3. Đồ thị độ dịch chuyển - thời gian

- Dùng đồ thị độ dịch chuyển – thời gian của chuyển động thẳng có thể mô tả được chuyển động: biết khi nào vật chuyển động, khi nào vật đổi chiều chuyển động, ....

- Vận tốc có giá trị bằng hệ số góc (độ dốc) của đường biểu diễn trong đồ thị độ dịch chuyển – thời gian của chuyển động thẳng.

4. Chuyển động biến đổi. Gia tốc

- Gia tốc là đại lượng cho biết sự thay đổi nhanh chậm của sự thay đổi vận tốc: $\overrightarrow a = \frac{{\Delta \overrightarrow v }}{{\Delta t}}$

- Khi $\overrightarrow a$ cùng chiều với ${\overrightarrow v }$ (a.v > 0): chuyển động nhanh dần; khi $\overrightarrow a$ ngược chiều với ${\overrightarrow v }$ (a.v < 0): chuyển động chậm dần

- Đơn vị của gia tốc trong hệ SI là m/s²(m.s^-2)

5. Chuyển động thẳng biến đổi đều

- Chuyển động thẳng biến đổi đều là chuyển động thẳng có gia tốc không đổi theo thời gian.

- Chuyển động thẳng nhanh dần đều có (a.v) > 0, chuyển động thẳng chậm dần đều có (a.v) < 0.

- Hệ số góc của đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều cho biết giá trị của gia tộc.

- Các công thức của chuyển động thẳng biến đổi đều:

1. v_t = v₀ + a.t

2. $d = {v_0}.t + \frac{1}{2}.a.{t^2}$

3. $v_t^2 - v_0^2 = 2.a.d$

6. Sự rơi tự do

- Chuyển động rơi chỉ chịu tác dụng của trọng lực gọi là rơi tự do.

- Chuyển động rơi tự do là chuyển động thẳng nhanh dần đều theo phương thẳng đứng, chiều từ trên xuống.

- Tại một nơi nhất định trên Trái Đất và ở gần mặt đất, mọi vật đều rơi tự do với cũng gia tốc g. Gia tốc rơi tự do ở các nơi khác nhau trên Trái Đất thì khác nhau.

- Các công thức của sự rơi tự do:

+ Gia tốc a = g = hằng số

+ Vận tốc tức thời: v_t = g.t

+ Độ lớn của độ dịch chuyển = Quãng đường đi được: $d = s = \frac{1}{2}.g.{t^2} = \frac{{v_t^2}}{{2.g}}$

7. Chuyển động ném

- Chuyển động ném có thể phân tích thành hai chuyển động thành phần vuông góc với nhau: chuyển động với gia tốc theo phương thẳng đứng, chuyển động thẳng đều theo phương nằm ngang.

- Các công thức của chuyển động ném:

+ Ném ngang:

Tầm xa: $L = {v_0}.t = {v_0}\sqrt {\frac{{2.H}}{g}}$

+ Ném xiên:

Tầm cao: $H = \frac{{v_{_0}^2.{{\sin }^2}\alpha }}{{2.g}}$

Tầm xa: $L = \frac{{v_{_0}^2.\sin 2\alpha }}{g}$

Chú ý: Các công thức trên chỉ đúng khi lực cản của không khí không đáng kể.

B. Bài tập minh họa

Bài 1. Hãy so sánh độ lớn của quãng đường đi được và độ dịch chuyển của ba chuyển động ở Hình 4.4 (phần bài tập ví dụ)

Hướng dẫn giải

- Quãng đường đi được từ ngắn đến dài: 2 – 1 – 3

- Độ dịch chuyển, ta thấy điểm đầu và điểm cuối của ba chuyển động đều như nhau nên độ dịch chuyển của ba chuyển động bằng nhau.

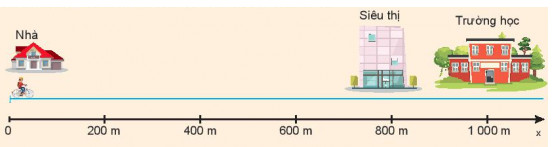
Bài 2: Hãy tính quãng đường đi được, độ dịch chuyển, tốc độ, vận tốc của bạn A khi đi từ nhà đến trường và khi đi từ trường đến siêu thị. Coi chuyển động của bạn A là chuyển động đều và cứ 100m bạn đi hết 25 giây

Hướng dẫn giải

a. Vì bạn A đi từ nhà đến trường là theo 1 hướng, không đổi hướng nên:

Quãng đường đi được và độ dịch chuyển là như nhau và bằng 1000m.

Vận tốc và tốc độ là như nhau và bằng : 100 : 25 = 4 m/s

b. Vì bạn A đi từ trường đến siêu thị là theo 1 hướng, không đổi hướng nên:

Quãng đường đi được và độ dịch chuyển là như nhau và bằng 1000 - 800 = 200 m.

Vận tốc và tốc độ là như nhau và bằng : 100 : 25 = 4 m/s.

Bài 3: Câu nào đúng?

A. Gia tốc của chuyển động thẳng nhanh dần đều bao giờ cũng lớn hơn gia tốc của chuyển động thẳng chậm dần đều.

B. Chuyển động thẳng nhanh dần đều có gia tốc lớn thì có vận tốc lớn.

C. Chuyển động thẳng biến đổi đều có gia tốc tăng, giảm đều theo thời gian.

D. Gia tốc trong chuyển động thẳng nhanh dần đều có phương, chiều và độ lớn không đổi.

Hướng dẫn giải

– Chọn đáp án D. Gia tốc trong chuyển động thẳng nhanh dần đều có phương, chiều và độ lớn không đổi.

– A, B sai vì tính chất nhanh dần chậm dần của chuyển động thẳng biến đổi đều chỉ xác định dựa vào dấu của tích a.v tại thời điểm mà ta xét. Do vậy ta không thể khẳng định được gia tốc của chuyển động thẳng nhanh dần đều bao giờ cũng lớn hơn gia tốc của chuyển động thẳng chậm dần đều hoặc chuyển động thẳng nhanh dần đều có gia tốc lớn thì có vận tốc lớn.

– C sai vì chuyển động thẳng biến đổi đều có vận tốc tăng, giảm đều theo thời gian (tức gia tốc a không thay đổi về độ lớn)

– D đúng vì trong chuyển động thẳng nhanh dần đều a.v > 0 nên phương và chiều của a cùng phương, cùng chiều với v, phương và chiều của v là phương và chiều của chuyển động.

------------------------------

Như vậy, VnDoc.com đã gửi tới các bạn Lý thuyết Vật lý 10 Bài tập cuối chương 2 KNTT. Ngoài ra, các em học sinh có thể tham khảo môn Vật lý 10 Cánh Diều, Hóa học 10 Cánh Diều và Toán 10 Chân trời sáng tạo tập 1, Sinh 10 Chân trời sáng tạo đầy đủ khác.

Đánh giá bài viết

1 24

Bài trước

Bài sau