Lý thuyết Vật lý 10 bài 20 KNTT

Một số ví dụ về cách giải các bài toán thuộc phần động lực học

1 412

VnDoc xin giới thiệu bài Lý thuyết Vật lý lớp 10 bài 20: Một số ví dụ về cách giải các bài toán thuộc phần động lực học được chúng tôi sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Vật lý lớp 10 sách Kết nối tri thức. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

Bài: Một số ví dụ về cách giải các bài toán thuộc phần động lực học

A. Lý thuyết Vật lý 10 bài 20
- 1.1. Các bước giải chính
- 2. Các loại bài toán
B. Bài tập minh họa

A. Lý thuyết Vật lý 10 bài 20

1.1. Các bước giải chính

- Chọn vật khảo sát chuyển động. Biểu diễn các lực tác dụng lên vật, trong đó làm rõ phương, chiều và điểm đặt của từng lực.

- Chọn hai trục vuông góc Ox và Oy; trong đó trục Ox cùng hướng với chuyển động của vật hay cùng hướng với lực kéo khi vật đứng yên. Phân tích các lực theo hai trục này. Áp dụng định luật 2 Newton theo hai trục tọa độ Ox và Oy.

$\left\{ {\begin{array}{*{20}{l}} {Ox:{\rm{ }}{F_x} - {F_{1x}}{\rm{ }} + {\rm{ }}{F_{2x}}{\rm{ }} + ... = m.{a_x}{\rm{ }}\left( 1 \right)}\\ {Oy:{\rm{ }}{F_y} = {F_{1y}}{\rm{ }} + {\rm{ }}{F_{2y}}{\rm{ }} + {\rm{ }}.. = 0{\rm{ }}\left( 2 \right)} \end{array}} \right.$

- Giải hệ phương trình (1) và (2) để tìm gia tốc hay tìm lực, tùy từng bài toán.

2. Các loại bài toán

a. Bài toán xác định gia tốc của vật khi biết lực tác dụng vào vật

Ví dụ. Một người đẩy một thùng hàng, khối lượng 50 kg, trượt trên sàn nhà. Lực đẩy có phương nằm ngang với độ lớn là 180 N. Tính gia tốc của thùng hàng, biết hệ số ma sát trượt giữa thùng hàng và sàn nhà là 0,25. Lấy g = 9,8 m/s².

Giải

Thùng hàng chịu tác dụng của bốn lực: trọng lực $\overrightarrow P$ , lực đẩy $\overrightarrow F$ , phản lực $\overrightarrow N$ và lực ma sát trượt $\overrightarrow F$ ms của sàn (Hình 20.1a).

Coi thùng hàng như một chất điểm (Hình 20.1b).

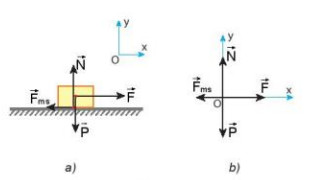
Hình 20.1

Áp dụng định luật 2 Newton cho chuyển động của vật theo hai trục Ox, Oy:

$\left\{ \begin{array}{l} Ox:{\rm{ }}{F_x} - F - {\rm{ }}{F_{ms}}{\rm{ }} = {\rm{ }}m.{a_x}{\rm{ }} - {\rm{ }}ma{\rm{ }}\left( 1 \right){\rm{ }}\\ Oy:{\rm{ }}{F_y} = N - P = 0 \end{array} \right.$

Giải hệ phương trình:

N=m.g = 50.9,8 = 490 N

F_ms = μ. N = 0,25.490 = 122,5 N

$a = \frac{{F - {F_{ms}}}}{m} = \frac{{180 - 122,5}}{{50}} = 1,15m/{s^2}$

Thùng hàng trượt với gia tốc a= 1,15 m/s² cùng chiều với trục Ox.

b. Bài toán xác định lực tác dụng vào vật khi biết gia tốc

Ví dụ 1. Một người dùng dây buộc để kéo một thùng gỗ theo phương nằm ngang bằng một lực $\overrightarrow F$ (Hình 20.2). Khối lượng của thùng là 35 kg. Hệ số ma sát giữa sàn và đáy thùng là 0,3. Lấy g = 9,8 m/s².

Tính độ lớn của lực kéo trong hai trường hợp:

a) Thùng trượt với gia tốc 0,2 m/s².

b) Thùng trộn đều.

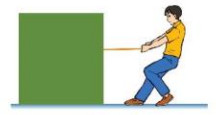
Hình 20.2

Giải

Thùng chịu tác dụng của bốn lực: trọng lực $\overrightarrow P = m.\overrightarrow g$ , lực kéo $\overrightarrow F$ , phản lực $\overrightarrow N$ và lực ma sát trượt $\overrightarrow Fms$ của mặt sản (Hình 20.3a).

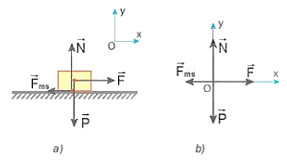
Hình 20.3

Coi thùng như một chất điểm (Hình 20.3b) và áp dụng định luật 2 Newton cho các lực thành phần theo các phương Ox, Oy.

$\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} Ox:{\rm{ }}{F_x}{\rm{ }} = {\rm{ }}F - {\rm{ }}{F_{ms}}{\rm{ }} = {\rm{ }}m{a_x}{\rm{ }} = {\rm{ }}ma{\rm{ }}\left( 1 \right){\rm{ }}\\ Oy:{\rm{ }}{F_y} = N - P = 0{\rm{ }}\left( 2 \right) \end{array}\\ {{F_{ms}} = \mu N\;} \end{array}} \right.$

Giải hệ phương trình:

Từ (2) → N = mg

Suy ra: F_ms = μN = μmg

Thay vào (1), ta được:

F = m.a + μ.m.g

F = m(a + μ.g)

a) Thùng trượt với gia tốc a= 0,2 m/s²

F= m(a + μ.g) = 35(0,2 +0,3.9,8) = 109,9 N.

b) Thùng trượt đều (a = 0)

F= μm.g = 0,3.35.9,8 = 102,9 N.

Ví dụ 2. Một chiếc hộp gỗ được thả trượt không vận tốc ban đầu, từ đầu trên của một tấm gỗ dài L= 2 m. Tấm gỗ đặt nghiêng 30° so với phương ngang. Hệ số ma sát giữa đáy hộp và mặt gỗ là 0,2. Lấy g = 9,8 m/s². Hỏi sau bao lâu thì hộp trượt xuống đến đầu dưới của tấm gỗ?

Giải

Hộp (coi là chất điểm) chịu tác dụng của ba lực: trọng lực $\overrightarrow P$ , phản lực $\overrightarrow N$ và lực ma sát trượt $\overrightarrow Fms$

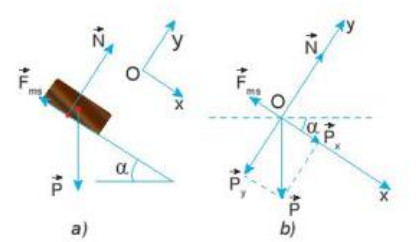
Hình 20.4

Phân tích trọng lực $\overrightarrow P$ thành hai lực thành phần $\overrightarrow Px$ , $\overrightarrow Py$ (Hình 20.4b) và áp dụng định luật 2 Newton theo hai trục Ox, Oy:

$\left\{ \begin{array}{l} Ox:{\rm{ }}{F_x}{\rm{ }} = {\rm{ }}m.g.sin\alpha - {F_{ms}} = m{a_x} = ma{\rm{ }}\left( 1 \right){\rm{ }}\\ Oy:{\rm{ }}{F_y} - N - m.g.cos\alpha {\rm{ }} = {\rm{ }}0\,\,\,(2)\\ {F_{ms}}{\rm{ }} = {\rm{ }}\mu N \end{array} \right.$

Giải hệ phương trình: $a = g(\sin \alpha - \mu \cos \alpha )$

Thay số, ta được: a = g(sin30^o – 0,2cos30^o)= 3,2 m/s²

Hộp trượt xuống với gia tốc a= 0,64 m/s², cùng chiều với trục Ox.

Áp dụng công thức:

$L = \frac{1}{2}a{t^2} \to t = \sqrt {\frac{{2L}}{a}} = \sqrt {\frac{{2.2}}{{3,2}}} \approx 1,1s$

B. Bài tập minh họa

Bài 1: Khối lượng Mặt Trăng nhỏ hơn khối lượng Trái Đất 81 lần, khoảng cách giữa tâm Trái Đất và tâm Mặt Trăng gấp 60 lần bán kính Trái Đất. Lực hút của Trái Đất và của Mặt Trăng tác dụng vào cùng một vật bằng nhau tại điểm nào trên đường thẳng nối tâm của chúng?

Hướng dẫn giải

Gọi khối lượng Mặt Trăng là M ⇒ khối lượng Trái Đất là 81 M

Bán kính Trái Đất là R thì khoảng cách giữa tâm Trái Đất và tâm Mặt Trăng là 60 R

Gọi h là khoảng cách điểm cần tìm đến tâm Trái Đất ⇒ khoảng cách từ điểm đó đến tâm Mặt Trăng là 60R - h (R, h > 0)

Theo bài ra: lực hút của Trái Đất tác dụng vào vật đó cân bằng với lực hút từ Mặt trăng tác dụng vào vật

F_hd1 = F_hd2

Bài 2: Một quyển sách được thả trượt từ đỉnh của một bàn nghiêng một góc α = 35° so với phương ngang. Hệ số ma sát trượt giữa mặt dưới của quyển sách với mặt bàn là μ = 0.5. Tìm gia tốc của quyển sách. Lấy g = 9.8 m/s2.

Hướng dẫn giải

Quyển sách chịu tác dụng của ba lực: trọng lực F , lực pháp tuyến N và lực ma sát Fms của mặt bàn.

Áp dụng định luật II Niu-tơn theo hai trục toạ độ.

Ox: Fx = Psinα – Fms = max = ma

Oy: Fy = N – Pcosα = may = 0

Fms = μN

Giải hệ phương trình ta được:

a = g. (sinα - μcosα) = 9.8.(sin35° - 0,50.cos35°)

⇒ a = l.6 m/s2, hướng dọc theo bàn xuống dưới.

Bài 3: Hai vật có khối lượng lần lượt là m₁= 5 kg và m₂= 10 kg được nối với nhau bằng một sợi dây không dãn và được đặt trên một mặt sàn nằm ngang. Kéo vật 1 bằng một lực $\overrightarrow F$ nằm ngang có độ lớn F = 45 N. Hệ số ma sát giữa mỗi vật và mặt sàn là $\mu = 0,2$ . Lấy $g = 9,8m/{s^2}$ . Tính gia tốc của mỗi vật và lực căng của dây nối.

Hướng dẫn giải

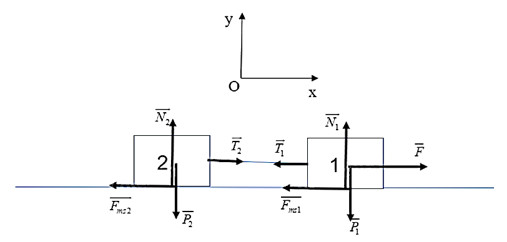
Chọn hệ quy chiếu như hình vẽ:

Theo định luật 2 Newton cho hệ vật, ta có:

$\overrightarrow {{P_1}} + \overrightarrow {{P_2}} + \overrightarrow {{N_1}} + \overrightarrow {{N_2}} + \overrightarrow F + \overrightarrow {{F_{ms1}}} + \overrightarrow {{F_{ms2}}} + \overrightarrow {{T_1}} + \overrightarrow {{T_2}} = ({m_1} + {m_2}).\overrightarrow a$ (1)

Chiếu (1) lên Ox, ta có

$\begin{array}{l}F - {F_{ms1}} - {F_{ms2}} - {T_1} + {T_2} = ({m_1} + {m_2}).a\\ \Leftrightarrow F - \mu ({N_1} + {N_2}) = ({m_1} + {m_2}).a\end{array}$

$\Leftrightarrow a = \frac{{F - \mu ({N_1} + {N_2})}}{{{m_1} + {m_2}}}$ (2)

(do ${T_1} = {T_2}$ )

Chiếu (1) lên Oy, ta có:

$\begin{array}{l}{N_1} + {N_2} - {P_1} - {P_2} = 0\\ \Leftrightarrow {N_1} + {N_2} = {P_1} + {P_2}\\ \Leftrightarrow {N_1} + {N_2} = ({m_1} + {m_2}).g\end{array}$

Thay ${N_1} + {N_2} = ({m_1} + {m_2}).g$ vào (2), ta có:

$\begin{array}{l}a = \frac{{F - \mu .g({m_1} + {m_2})}}{{{m_1} + {m_2}}}\\ \Leftrightarrow a = \frac{{45 - 0,2.9,8.(5 + 10)}}{{5 + 10}}\\ \Leftrightarrow a = 1,04(m/{s^2})\end{array}$

Xét vật 1

Theo định luật 2 Newton, ta có

$\overrightarrow {{P_1}} + \overrightarrow {{N_1}} + \overrightarrow F + \overrightarrow {{F_{ms1}}} + \overrightarrow {{T_1}} = {m_1}.\overrightarrow a$ (3)

Chiếu (3) lên Ox, có

$\begin{array}{l}F - {F_{ms1}} - {T_1} = {m_1}.a\\ \Leftrightarrow {T_1} = F - \mu {N_1} - {m_1}.a\end{array}$

Chiếu (3) lên Oy, ta có ${N_1} = {P_1} = {m_1}.g$

$\begin{array}{l} \Rightarrow {T_1} = F - \mu {m_1}g - {m_1}.a\\ \Leftrightarrow {T_1} = 45 - 0,2.5.9,8 - 5.1,04\\ \Leftrightarrow {T_1} = 30(N)\end{array}$