Bài tập Số nguyên tố nâng cao
Bài tập Số nguyên tố nâng cao
Bài tập Số nguyên tố nâng cao được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 6 hiệu quả hơn. Mời các bạn tham khảo.
1. Số nguyên tố
− Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Bất kỳ số tự nhiên lớn hơn 1 nào cũng có ít nhất một ước số nguyên tố
Ví dụ:
Số 5 có hai ước là 1 và 5 nên 5 là số nguyên tố.
2. Hợp số
− Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.
Ví dụ:
Số 9 có các ước là 1, 3, 9 nên 9 là hợp số.
Chú ý: Các số 0 và 1 không phải là số nguyên tố cũng không phải là hợp số
Nhận xét:
Cách kiểm tra một số là số nguyên tố: Để kết luận số a là số nguyên tố (a > 1), chỉ cần chứng tỏ rằng nó không chia hết cho mọi số nguyên tố mà bình phương không vượt quá a.
3. Số nguyên tố cùng nhau
1 - Hai số tự nhiên được gọi là nguyên tố cùng nhau khi và chỉ khi chúng có ước chúng lớn nhất bằng 1
a, b nguyên tố cùng nhau ⇒ (a, b) = 1 (a, b ∈ N)
2 - Hai số tự nhiên liên tiếp luôn nguyên tố cùng nhau
3 - Hai số nguyên tố khác nhau luôn nguyên tố cùng nhau
4 - Các số a, b, c nguyên tố cùng nhau ⇒ (a, b, c) = 1
5 - a, b, c nguyên tố sánh đôi khi chúng đôi một nguyên tố cùng nhau
a, b, c nguyên tố sánh đôi ⇒ (a, b) = (b, c) = (a, c) = 1
4. Phân tích một số tự nhiên ra thừa số nguyên tố
Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Chú ý:
+ Dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính số đó.
+ Mọi hợp số đều phân tích được ra thừa số nguyên tố.
4.1. Cách phân tích một số ra thừa số nguyên tố theo sơ đồ cây
Để phân tích một số ra thừa số nguyên tố theo sơ đồ cây, ta trình bày như sau:
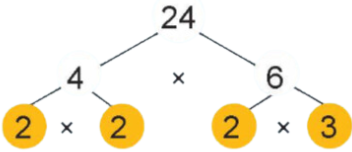
hoặc
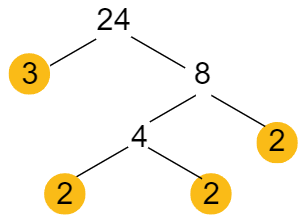
Vậy 24 = 23 . 3
4.2. Cách phân tích một số ra thừa số nguyên tố theo sơ đồ cột
Ta có thể phân tích theo chiều dọc như sau:
Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
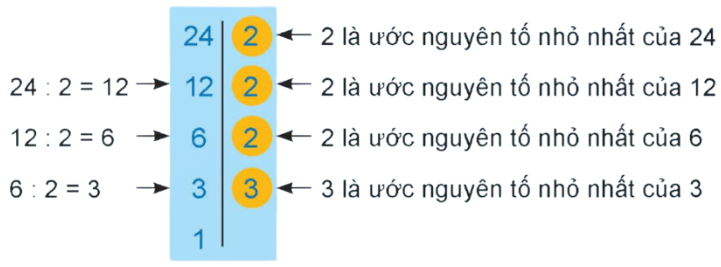
Như vậy 24 = 23 . 3
Nhận xét: Dù phân tích một số ra thừa số nguyên tố bằng cách nào đi nữa thì cuối cùng cũng ra một kết quả.
5. Bài tập
Bài 1: Chứng minh rằng các tổng sau đây là hợp số:
a) A = 27 + 311 + 513 + 717 + 1119
b) B = 1 + 2123 + 23124 + 25125
Lời giải:
a) 27 + 311 + 513 + 717 + 1119
Ta có: 27 có chữ số tận cùng là 8
311 có chữ số tận cùng là 7
513 luôn có chữ số tận cùng là 5
717 có chữ số tận cùng là 7
1119 luôn có chữ số tận cùng là 1
Do đó: Tổng A có chữ số tận cùng là 8
Suy ra A chia hết cho 2.
Vậy, A là hợp số.
b) Ta có: 1 + 2123 + 23124 + 25125
Ta có: 2123 có chữ số tận cùng là 1
23124 có chữ số tận cùng là 1
25125 luôn có chữ số tận cùng là 5
Do đó: Tổng B có chữ số tận cùng là 8
Suy ra B chia hết cho 2.
Vậy, B là hợp số.
Bài 2: Tìm n ∈ N* để n4 + 4 là số nguyên tố.
Lời giải:
Ta có: n4 + 4 = (n4 + 4n2 + 4) – 4n2
= (n2 + 2)2 – (2n)2
= (n2 + 2 + 2n)(n2 + 2 – 2n)
Nếu n4 + 4 là số nguyên tố thì n2 – 2n + 2 = 1 ⇒ n = 1
Thử lại: Với n = 1 thì n4 + 4 = 5 là số nguyên tố
Vậy với n = 1 thì n4 + 4 = 5 là số nguyên tố.
Bài 3: Tìm số nguyên tố p sao cho p + 10 và p + 14 là các số nguyên tố.
Lời giải:
• Với p = 3 thì p + 3 = 13 và p + 14 = 17 là các số nguyên tố
• Với p > 3 thì p = 3k ± 1
Nếu p = 3k + 1 thì p + 14 = 3k + 15 ⋮ 3
Nếu p = 3k – 1 thì p + 10 = 3k + 9 ⋮ 3
Vậy với p = 3 thì p + 10 và p + 14 là số nguyên tố.
–––––––––––––––––––––––––––––––








