Bài tập Toán lớp 6: Phép cộng, trừ các số nguyên

Bài tập Toán lớp 6: Phép cộng, trừ các số nguyên gồm các dạng bài tập hình học Chương 2 lớp 6 về số nguyên giúp cho các em học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán lớp 6. Mời các em học sinh tham khảo chi tiết.

I. Các dạng bài tập thường gặp

Dạng 1: Thực hiện phép tính cộng

• Cộng hai số nguyên dương thì giống với cộng hai số tự nhiên.

Chẳng hạn: 2 + 3 = 5.

• Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng lại rồi đặt dấu trừ (-) trước kết quả.

Tức là:

(-a) + (-b) = -(a + b)

• Muốn cộng hai số nguyên khác dấu, ta phải làm hai bước:

+) Bước 1 – Tìm dấu của tổng: Dấu của tổng giống với dấu của số hạng có phần số tự nhiên lớn hơn.

+) Bước 2 – Lấy phần số tự nhiên lớn trừ cho phần số tự nhiên nhỏ, rồi đặt dấu đã tìm được ở Bước 1 vào trước kết quả.

Dạng 2: Tìm số đối

Muốn tìm số đối của một số nguyên, ta chỉ cần đổi dấu của số nguyên đó (và giữ nguyên phần số tự nhiên).

Lưu ý: Số đối của 0 là 0.

Dạng 3: Thực hiện phép trừ

Muốn tìm a – b, ta lấy a cộng với số đối của b. Tức là:

a – b = a + (-b)

II. Các ví dụ minh họa

1. Cộng hai số nguyên cùng dấu

Quy tắc cộng hai số nguyên âm

Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi đặt dấu “-“ trước kết quả.

Ví dụ 1. Tính:

a) (-23) + (-55); b) 43 + 23; c) (-234) + (-546).

Lời giải

a) (-23) + (-55) = - (23 + 55) = - 78;

b) 43 + 23 = 66;

c) (-234) + (-546) = - (234 + 546) = - 780.

2. Cộng hai số nguyên khác dấu

Hai số đối nhau:

Hai số nguyên a và b được gọi là đối nhau nếu a và b nằm khác phía với điểm 0 và có cùng khoảng cách đến gốc 0.

Chú ý:

Ta quy ước số đối của 0 là chính nó.

Tổng của hai số đối nhau luôn bằng 0.

Ví dụ 2. Tìm số đối của -3; 4; -5; 8; -12.

Lời giải

Số đối của – 3 là 3;

Số đối của 4 là -4;

Số đối của – 5 là 5;

Số đối của 8 là – 8;

Số đối của -12 là 12.

Quy tắc cộng hai số nguyên khác dấu:

+ Hai số nguyên đối nhau thì có tổng bằng 0.

+ Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phân số tự nhiên của chúng (số lớn trừ số nhỏ) rồi đặt trước hiệu tìm được dấu của số có phần số tự nhiên lớn hơn.

Ví dụ 3. Thực hiện các phép tính:

a) 312 + (-134); b) (– 254) + 128; c) 2 304 + (-115).

Lời giải

a) 312 + (-134) = 312 – 134 = 178;

b) (– 254) + 128 = - ( 254 – 128) = -128;

c) 2 304 + (-115) = 2 304 – 115 = 2 189.

3. Tính chất của phép cộng

Phép cộng số nguyên có tính chất sau:

+ Giao hoán: a + b = b + a;

+ Kết hợp: (a + b) + c = a + (b + c).

Ví dụ 4. Tính một cách hợp lí:

a) (-350) + (-296) + 50 + 96;

b) (-3) + 5 + (-7) + 5.

Lời giải

a) (-350) + (-296) + 50 + 96

= [(-350) + 50] + [(-296) + 96]

= (-300) + (-200)

= -500.

b) (-3) + 5 + (-7) + 5

= [(-3) + (-7)] + [5 + 5]

= (-10) + 10

= 0.

4. Trừ hai số nguyên

Quy tắc trừ hai số nguyên

Muốn trừ số nguyên a cho số nguyên b, ta cộng số nguyên a với số đối của số nguyên b:

a – b = a + (-b).

Ví dụ 5. Tính:

a) 15 – 7; b) 8 – 9; c) 23 – 154; d) 12 – 125 – 83.

Lời giải

a) 15 – 7 = 8;

b) 8 – 9 = 8 + (-9) = - (9 – 8) = -1;

c) 23 – 154 = - ( 154 – 23) = -131;

d) 12 – 125 – 83

= 12 + (-125) + (-83)

= -(125 – 12) + (-83)

= (-113) + (-83)

= -(113 + 83)

= - 196.

III. Bài tập Phép cộng, phép trừ số nguyên - Toán lớp 6

Bài toán 1: Tính.

a) (-34) + (-91) + (-26) + (-99)

b) 125 + |-25|

c) |-26| + |-34|

d) |-82| + (-120)

e) (-275) + |-115|

f) (-34) + |-34|

Bài toán 2: Tính nhanh.

a) 123 + [54 + (-123) + 46]

b) -64 + [(-111) + 64 + 71]

Bài toán 3: Tính.

a) (-354) – (+75)

b) (-445) – (-548)

c) |-72| – (+455)

d) -|-1945| – |-67|

Bài toán 4: Tính.

a) (-35) + 23 – (-35) – 47

b) 24 – (-136) – (-70) + 15 + (-115)

c) 37 – (-43) + (-85) – (-30) + 15

Bài toán 5: Tìm các số nguyên x, biết.

a) x + (-13) = – 144 – (-78)

b) x + 76 = 58 – (-16)

c) 453 + x = -44 – (-199)

d) |-x + 8| = 12

e) |x + 8| + 8 = 7

f) -8.|x| = -104

Bài toán 6: Tính tổng các số nguyên x, biết.

a) – 5 < x < 4

b) – 5 ≤ x ≤ 5

c) – 15 ≤ x < 20

d) -24 < x ≤ 18

e) – 17 < x < 0

g) – 20 ≤ x < 21

Bài toán 7: Tính các tổng sau đây một cách hợp lí.

a) 12 + 22 + (-20) + (-153) + 8

b) 9 + (-10) + 11 + (-12) + 13 + (-14) + 15 + (-16)

c) 371 + (-271) + (-531)

Bài toán 8: Tính nhanh.

a) [128 + (-78) + 100] + (-128)

b) 125 + [(-100) + 93] + (-218)

c) [453 + 74 + (-79)] + (-527)

Bài toán 9: Tìm các số nguyên x, biết.

a) 484 + x = -363 – (-548)

b) |x + 9| = 12

c) |2x + 9| = 15

d) 25 – |3 – x| = 10

Bài toán 10: Bỏ dấu ngoặc rồi tính.

a) (123 – 27) + (27 + 13 – 123)

b) (175 + 25 + 13) – (-15 + 175 + 25)

c) (2012 – 119 + 29) – (-119 + 29)

d) – (55 – 80 + 91) – (2012 + 80 – 91)

Bài toán 11: Cho x, y là các số nguyên.

a) Tìm GTNN của A = |x + 2| + 50

b) Tím GTNN của B = |x – 100| + |y + 200| – 1

c) Tìm GTLN của 2015 – |x + 5+|

Bài toán 12:

a) Tìm các số nguyên x sao cho (x – 5) là ước của 6.

b) Tìm các số nguyên x sao cho (x – 1) là ước của 15.

c) Tìm các số nguyên x sao cho (x + 6) chia hết cho (x + 1)

Bài toán 13: Tính tổng : S = 1 – 2 + 3 – 4 + … + 99 – 100.

Bài toán 14: Tính tổng:

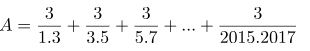
Bài toán 15: Tìm x, y ∈ Z biết.

a) (x + 1)(y – 2) = 0

b) (x – 5)(y – 7) = 1

c) (x + 4)(y – 2) = 2

d) (x + 3)(y – 6) = -4

e) (x + 7)(5 – y) = -6

f) (12 – x)(6 – y) = -2

Bài toán 16: Tính: 12 – (10 – 19).

Bài toán 17: Tìm số đối của:

a) 14 + 27;

b) 19 + (-5);

c) -56 + (-13).

............................

Trên đây, VnDoc đã gửi tới các bạn Bài tập Toán lớp 6: Phép cộng, trừ các số nguyên. Hy vọng đây là tài liệu hay giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt Toán 6 hơn.