Đề kiểm tra học kì 1 môn Toán lớp 12 năm học 2014 - 2015 trường THPT Châu Thành 1, Đồng Tháp
Đề kiểm tra học kì 1 môn Toán lớp 12
Đề kiểm tra học kì 1 môn Toán lớp 12 năm học 2014 - 2015 trường THPT Châu Thành 1, Đồng Tháp có đáp án là tài liệu tham khảo hữu ích dành cho các bạn học sinh lớp 12, giúp các bạn ôn tập và củng cố kiến thức, từ đó, chuẩn bị tốt nhất cho kì thi học kì 1 sắp diễn ra. Chúc các bạn học tốt.
Đề thi học kì 1 môn Tiếng Anh lớp 12 trường THPT Châu Thành 1, Đồng Tháp năm 2014 - 2015
Đề thi học kỳ I lớp 12 THPT chuyên Thái Nguyên năm 2012 - 2013
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH ĐỒNG THÁP
ĐỀ CHÍNH THỨC (Đề gồm có 01 trang) |
KIỂM TRA HỌC KÌ I Năm học: 2014-2015 Môn thi: TOÁN - Lớp 12 Ngày thi: 11/12/2014 Thời gian: 120 phút (không kể thời gian phát đề) |
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)
Câu I. (3,0 điểm) Cho hàm số y = x4 - (m + 3)x2 + m + 2 (1); m là tham số thực.
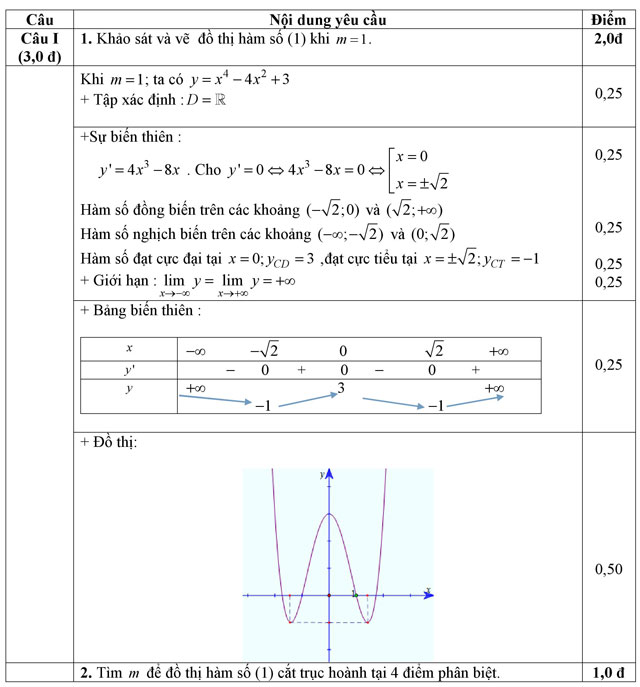
- Khảo sát và vẽ đồ thị hàm số (1) khi m = 1.
- Tìm tất cả các giá trị của m để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt.
Câu II. (2,0 điểm)
- Tính giá trị biểu thức P = esin2x (ecos2x - e-sin2x) - 10loge + (2014)ln1.
- Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
.
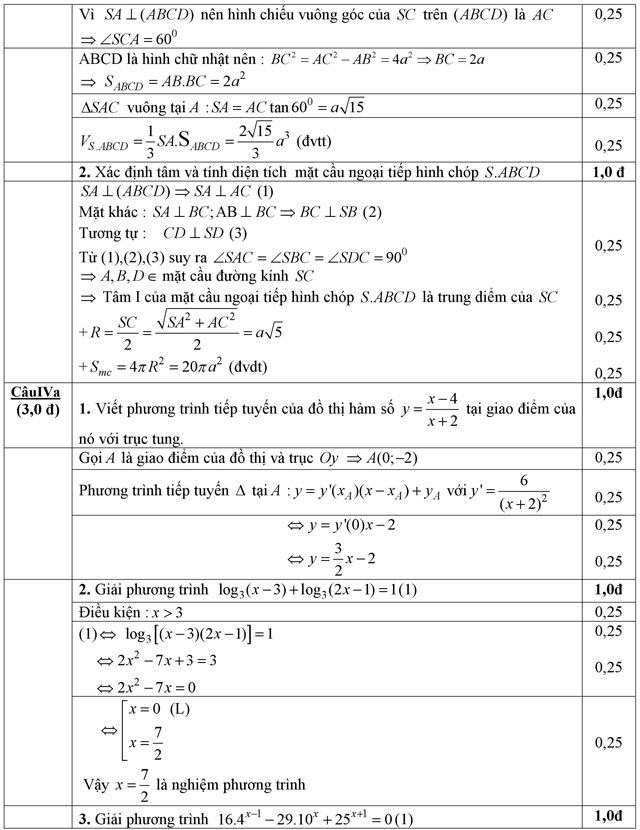
.Câu III. (2,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật; AB = a và AC = a√5. Cạnh SA vuông góc mặt phẳng (ABCD); cạnh SC tạo với mặt phẳng đáy một góc bằng 600.
- Tính theo a thể tích khối chóp S.ABCD.
- Xác định tâm và tính diện tích mặt cầu ngoại tiếp hình chóp .
II. PHẦN RIÊNG - Tự chọn (3,0 điểm)
Thí sinh chỉ chọn một trong hai câu (câu IV.a hoặc câu IV.b)
Câu IV.a. Theo chương trình Chuẩn (3,0 điểm)
- Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của nó với trục tung.
- Giải phương trình log3(x - 3) + log3(2x - 1) = 1.
- Giải phương trình 16.x4-1 - 29.10x + 25x+1 = 0.
tại giao điểm của nó với trục tung.Câu IV.b. Theo chương trình Nâng cao (3,0 điểm)
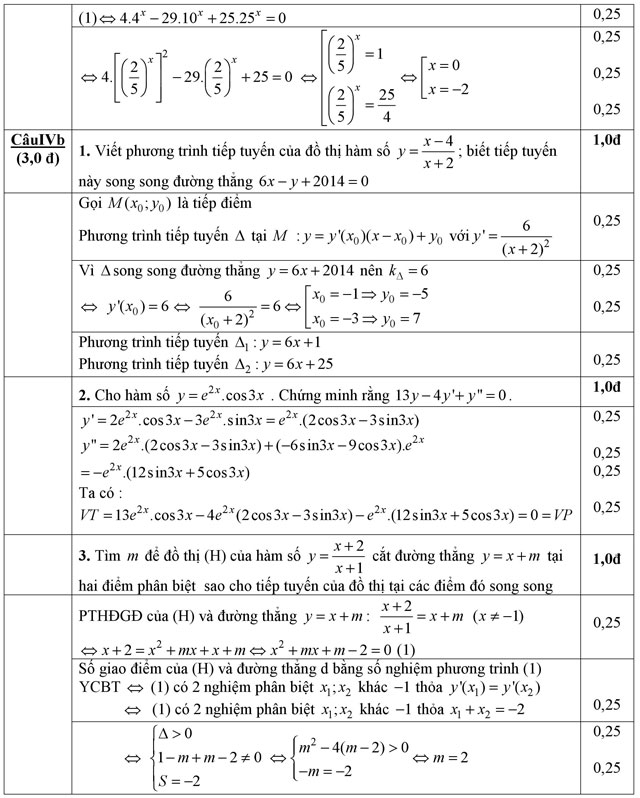
- Viết phương trình tiếp tuyến của đồ thị hàm số ; biết rằng tiếp tuyến này song song đường thẳng 6x - y + 2014 = 0.
- Cho hàm số y = e2x .cos3x. Chứng minh rằng 13y - 4y' + y'' = 0.
- Tìm m để đồ thị (H) của hàm số cắt đường thẳng y = x + m tại hai điểm phân biệt A, B sao cho tiếp tuyến của đồ thị (H) tại các điểm đó song song.
cắt đường thẳng y = x + m tại hai điểm phân biệt A, B sao cho tiếp tuyến của đồ thị (H) tại các điểm đó song song.Đáp án đề kiểm tra học kì 1 môn Toán lớp 12
