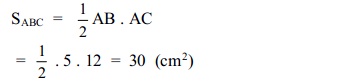Đề thi học kì 1 môn Toán lớp 8 huyện Tân Châu, Tây Ninh năm 2015 - 2016
Đề thi học kì 1 môn Toán lớp 8 năm 2015 - 2016
Đề thi học kì 1 môn Toán lớp 8 huyện Tân Châu, Tây Ninh năm 2015 - 2016 gồm 2 câu hỏi lý thuyết và 5 câu hỏi bài tập có đáp án đi cùng. Đề thi sẽ giúp các bạn luyện tập và củng cố kiến thức môn Toán hiệu quả. Mời các bạn tham khảo.
Đề thi học kì 1 môn Toán lớp 8 Phòng GD và ĐT Bảo Lộc trực tuyến
Đề thi học kì 1 môn Toán lớp 8 năm 2014 - 2015 online
Đề thi học kì 1 môn Toán lớp 8 trường THCS Lương Phú, Thái Nguyên năm 2015 - 2016
|
UBND HUYỆN TÂN CHÂU PHÒNG GIÁO DỤC VÀ ĐÀO TẠO |
CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM Độc lập – Tự do – Hạnh phúc |
KỲ KIỂM TRA HỌC KỲ I NĂM HỌC 2015 - 2016
Môn: Toán - Lớp 8
Thời gian: 90 phút
(Không kể thời gian phát đề)
I/ Lý thuyết: (2 điểm)
Câu 1: (1,0 điểm)
a) Viết hằng đẳng thức lập phương của một hiệu.
b) Áp dụng tính: (x - 2)3
Câu 2: (1,0 điểm)
Phát biểu dấu hiệu nhận biết hình thoi.
II/ Bài tập: (8 điểm)
Bài 1: (1,5 điểm)
Phân tích các đa thức sau thành nhân tử:
a) x2 - xy + x - y
b) 5x3 - 10x2y + 5xy2
Bài 2: (2 điểm)
Thực hiện các phép tính sau:
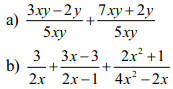
Bài 3: (1 điểm)
Tìm x, biết: 5x(x – 1) = x - 1
Bài 4: (0,5 điểm)
Tìm n ∈ Z để 2n2 – n + 2 chia hết cho 2n + 1.
Bài 5: (3,0 điểm)
Cho tam giác ABC vuông tại A (AB < AC). Điểm M là trung điểm của cạnh BC. Vẽ MD vuông góc với AB tại D, ME vuông góc với AC tại E. Trên tia đối của tia DM lấy điểm N sao cho DN = DM.
a) Chứng minh rằng: tứ giác ADME là hình chữ nhật.
b) Chứng minh rằng: tứ giác AMBN là hình thoi.
c) Cho AB = 5cm; BC = 13cm. Tính diện tích tam giác ABC.
Đáp án đề thi học kì 1 môn Toán lớp 8
I. Lý thuyết:
Câu 1 (1,0 điểm)
a) (A - B)3 = A3 - 3A2B + 3AB2 – B3
b) (x - 2)3 = x3 - 6x2 + 12x - 8
Câu 2 (1,0 điểm)
Phát biểu đúng dấu hiệu SGK Toán 8 Học kì I (trang 105).
II. Bài tập:
Bài 1 (1,5 điểm)
a) x2 - xy + x - y
= (x2 – xy) + (x – y)
= x(x – y) + (x – y)
= (x – y)(x + 1)
b) 5x3 - 10x2y + 5xy2
= 5x(x2 – 2xy +y2)
= 5x(x – y)2
Bài 2 (2 điểm)
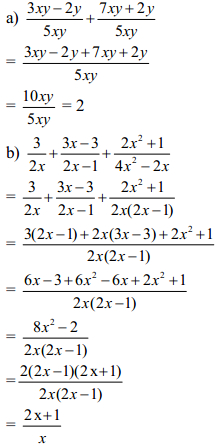
Bài 3 (1 điểm)
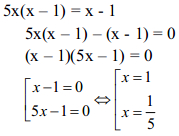
Bài 4 (0,5 điểm)
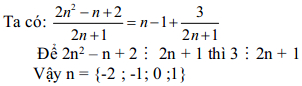
Bài 5 (3,0 điểm)
HS vẽ hình ghi GT, KL
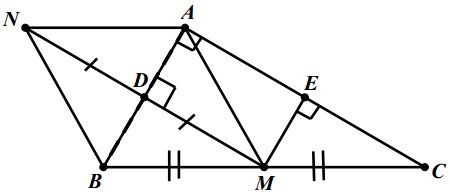
a) Chứng minh Tứ giác ADME là hình chữ nhật:
Ta có: ![]() (gt)
(gt)
Nên tứ giác ADME là hình chữ nhật (tứ giác có 3 góc vuông)
b) Chứng minh Tứ giác AMBN là hình thoi:
Xét ABC, ta có: MB = MC (gt) và MD // AC (cùng AB)
Suy ra: MD là đường trung bình của tam giác ABC
Hay: AD = DB (1)
Ta lại có DM = DN (gt)
Nên tứ giác AMBN là hình bình hành (tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Mà AB ⊥ MN (gt)
Do đó tứ giác AMBN là hình thoi (hình bình hành có hai đường chéo vuông góc)
c) Tính diện tích tam giác ABC biết AB = 5cm, BC = 13cm.
Áp dụng định lí Pytago cho ABC, vuông tại A.Ta có:
AC2 = BC2 – AB2 = 132 – 52 = 169 – 25 = 144
=> AC = 12(cm)