VnDoc.com

Đề thi học kì 2 lớp 9 môn Toán Phòng GD&ĐT Quận Hoàn Kiếm năm học 2018 - 2019

Đề kiểm tra học kì 2 toán 9 năm 2019 có đáp án

VnDoc.com

UBND QUẬN HOÀN KIẾM

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO

ĐỀ KIỂM TRA HỌC KÌ II

MÔN TOÁN LỚP 9 NĂM HỌC 2018 - 2019

Ngày kiểm tra: 19/4/2019

Thời gian làm bài: 90 phút (Không kể thời gian phát đề)

Bài I (2,0 điểm). Cho hai biểu thức:

x

A

x







34

1

và

  

  

   

2 4 2 1

( 1)( 2) 1 2

x x x

B

x x x x

với

0; 4.xx

1) Tính giá trị của

A

khi

x  9.

2) Rút gọn

B

và biểu thức

P A B ..

3) Tìm

x

để

P  2

.

Bài II (2,0 điểm). Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Để đóng gói hết

600

tập vở tặng các bạn nghèo vùng cao, lớp

9A

dự định dùng một số thùng

carton cùng loại, số tập vở trong mỗi thùng là như nhau. Tuy nhiên, khi đóng vở vào các thùng, có

3

thùng bị hỏng, không sử dụng được nên mỗi thùng còn lại phải đóng thêm

10

tập vở nữa mới hết.

Tính số thùng carton ban đầu lớp

9A

dự định sử dụng và số tập vở dự định đóng trong mỗi thùng.

Bài III (2,0 điểm).

1) Giải hệ phương trình:

1

2 1 5

3

.

3

5 1 13

3

x

y

x

y



  











  







2) Cho phương trình

 

2

2 2 2 5 0m x mx     

với ẩn x.

a) Giải phương trình với

2.m

b) Tìm m để phương trình có hai nghiệm phân biệt

12

,xx

thỏa mãn

12

2xx

.

Bài IV (3,5 điểm). Cho đường tròn

()O

, dây

BC

cố định. Trên cung lớn

BC

của

()O

, lấy điểm

A

( , )A B A C

sao cho

AB AC

. Hai tiếp tuyến qua

B

và

C

của

()O

cắt nhau tại

E

.

1) Chứng minh tứ giác

BOCE

nội tiếp.

2)

AE

cắt

()O

tại điểm thứ hai

D

()DA

. Chứng minh

2

..EB ED EA

3) Gọi

F

là trung điểm của

AD

. Đường thẳng qua

D

và song song với

EC

cắt

BC

tại

G

.

Chứng minh

GF

song song với

.AC

4) Trên tia đối của tia

AB

lấy điểm

H

sao cho

AH AC

. Chứng minh khi điểm

A

thay

đổi trên cung lớn

BC

thì điểm

H

di động trên một đường tròn cố định.

Bài V (0,5 điểm). Cho ba số thực dương

a,b,c

thỏa mãn

1 1 2

.

a c b



Tìm giá trị nhỏ nhất của

biểu thức

a b c b

K

2a b 2c b







.

----- HẾT -----

Họ và tên học sinh: ………………………… Trường: ………………..………… SBD: ..……

Chữ kí của giám thị 1: ………………… Chữ kí của giám thị 2: …………...……

Chúc các em học sinh làm bài đạt kết quả tốt./.

ĐỀ CHÍNH THỨC

VnDoc.com

UBND QUẬN HOÀN KIẾM

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO

HƯỚNG DẪN CHẤM

ĐỀ KIỂM TRA HỌC KÌ II

MÔN TOÁN LỚP 9 NĂM HỌC 2018 - 2019

Ngày kiểm tra: 19/4/2019

Bài

Nội dung

Điểm

Bài I

2 điểm

1) (0,5đ)

Thay

9x 

(TMĐK) vào biểu thức

A

0,25

3 9 4 5

.

4

91

A







0.25

2) (1đ)

  

     



  

  

     

22

2 4 1

1 2 1 2 1 2

xx

x x x

B

x x x x x x

0,25

     

2 4 4 1 2 1

2 1 2 1

x x x x x x

x x x x

       



   

0,25

 

  

2

1

2

21

x

xx









0,25

34

.

2

x

P

x







0,25

3) (0,5đ)

Ta có

34

2 0 2 0 0.

22

xx

P

xx



      



Trường hợp 1:

00xx  

(TMĐK)

0,25

Trường hợp 2:

0x 

0 2 0 4

2

x

xx

x

      



(TMĐK)

Kết hợp điều kiện, ta có với

0x 

hoặc

4x 

thì

 2.P

0,25

Bài II.

1,5đ

Cách 1.

Gọi số thùng carton ban đầu lớp 9A sử

dụng là

x

(

*, 3x N x

, thùng).

Cách 2.

Gọi số thùng carton ban đầu

lớp 9A sử dụng là

x

(

*, 3x N x

, thùng).

0,25

 Số tập vở trong mỗi thùng là

600

x

(tập vở)

Gọi số tập vở trong mỗi thùng

là

y

(

*yN

, tập vở)

0,25

Số thùng carton thực tế sử dụng là

3x

(thùng).

Thực tế, mỗi thùng đóng số tập vở là

600

10

x









(tập vở).

Số thùng carton thực tế sử

dụng là

3x

(thùng).

Thực tế,, mỗi thùng đóng số

tập vở là

10y 

(tập vở).

0,5

Vì thực tế vẫn đóng hết số

600

tập vở

nên ta có phương trình:

Lập luận ra các phương trình :

600xy 

0,25

VnDoc.com

 

600

3 10 600x

x



  





và

  

3 10 600.xy  

Ta có hệ phương trình

  

600

3 10 600

xy









  





Giải phương trình được:

1

15x 

(TMĐK);

2

12x 

(loại)

 Số tập vở trong mỗi thùng là 40 tập

vở.

Giải hệ phương trình được

1

15x 

(TMĐK);

2

12x 

(loại) 

40y 

(TMĐK).

0,5

Kết luận: Vậy số thùng ban đầu là:

15

thùng, số tập vở dự định trong mỗi

thùng là

40

tập vở.

0,25

Bài III.

2,5đ

1) (1đ)

1) ĐKXĐ:

1, 3.xy

0,25

Đặt

1

1;

3

x a b

y





25

.

5 3 13

ab













0,25

Giải ra ta được:

2

1

a

b











(TMĐK).

0,25

Từ đó tìm được

5

4

x

y











(TMĐK).

Vậy nghiệm của hệ phương trình là (5 ; 4).

0,25

2)

2a (0,5đ)

Cách 1.

Xét

1 2 2 4 2 2 5 0a b c       

Cách 2.

Ta có:

 

2

' 11 6 2 3 2    

0,25

Phương trình có hai nghiệm

12

1; 2 2 5xx   

Kết luận.

0,25

2b (0,5đ)

Cách 1.

Xét

1 2 4 2 5 0a b c m m       

Suy ra phương trình có hai nghiệm:

12

1; x 2 5xm   

Phương trình có hai nghiệm phân biệt

12

3.x x m    

Cách 2.

Phương trình có hai nghiệm

phân biệt

2

10

' (m 3) 0

3.

a

m









   



  

0,25

Ta có:

12

2521xx m   

 

2

.

3

m TMĐK

m KTMĐK















Kết luận:

2.m 

Áp dụng hệ thức Vi-ét ta có:

12

24

. 2 5

x x m

  





  



Ta có:

12

2xx

22

1 2 1 2

2 . 4x x x x   

 

2

4 20 22

2 2 5 30

mm

m

  

  

Tìm được

 

2.m

0,25

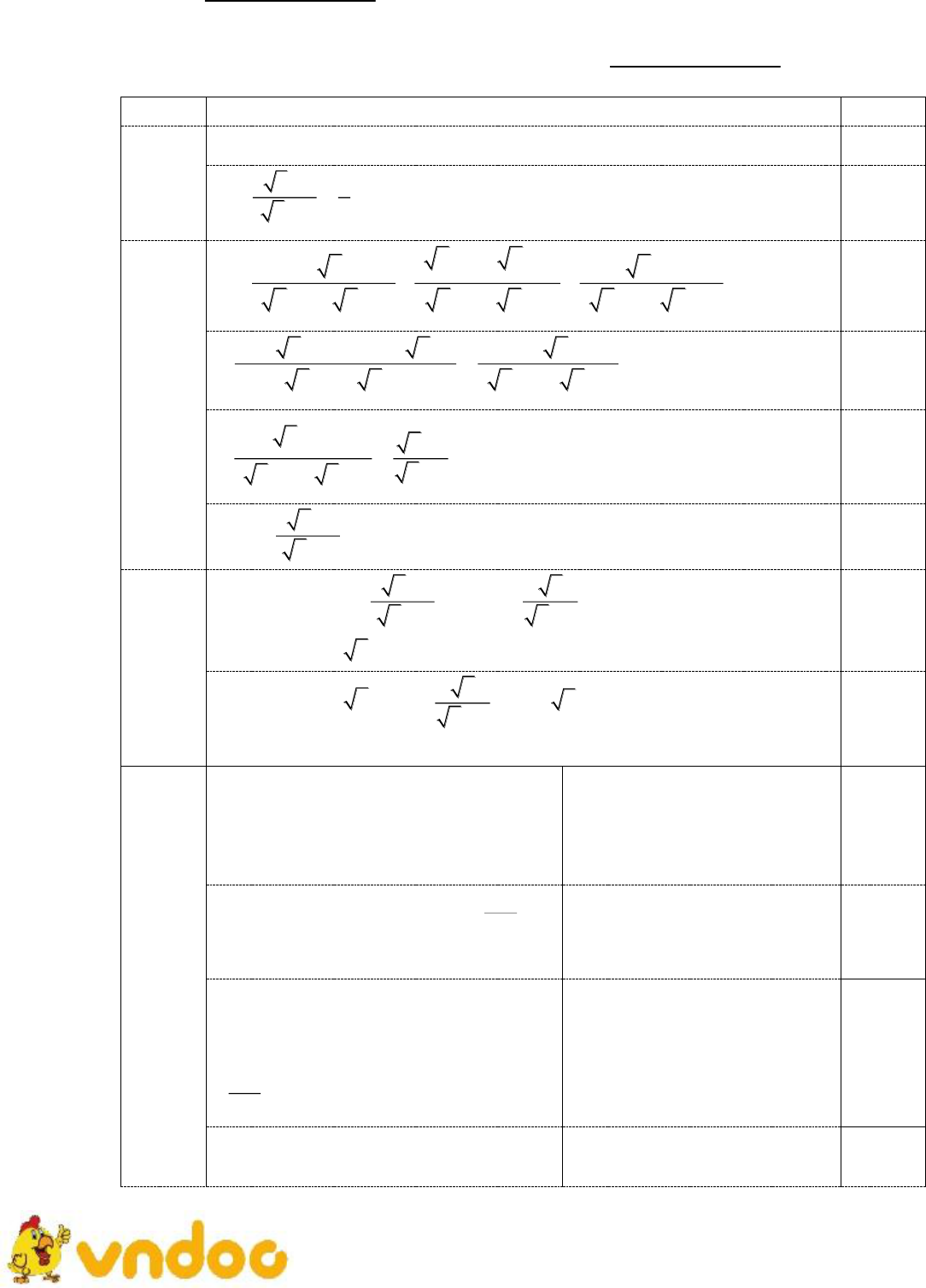
Đề thi học kì 2 lớp 9 môn Toán Phòng GD&ĐT Quận Hoàn Kiếm năm 2018

Đề thi học kì 2 lớp 9 môn Toán Phòng GD&ĐT Quận Hoàn Kiếm năm học 2018 - 2019 là đề thi học kì 2 lớp 9 được VnDoc sưu tầm và đăng tải. Hy vọng tài liệu này sẽ giúp ích cho các bạn ôn tập và rèn luyện chuẩn bị kì thi cuối kì được tốt. Mời các bạn tải về tham khảo

Đề thi học kì 2 lớp 9 môn Toán Phòng GD&ĐT Quận Hoàn Kiếm năm học 2018 - 2019

.......................................................................

Ngoài Đề thi học kì 2 lớp 9 môn Toán Phòng GD&ĐT Quận Hoàn Kiếm năm học 2018 - 2019. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt